BuilderBoi

Alright, I'll take a shot. 

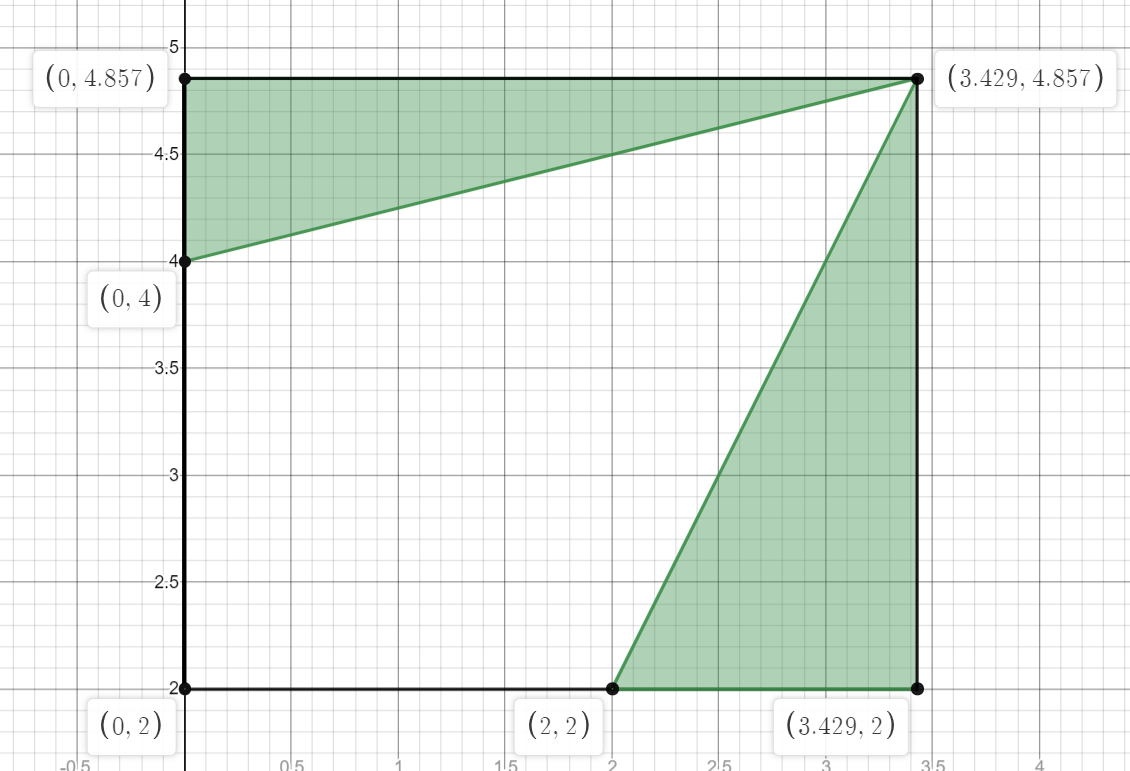
It helps to inscribe the trapezoid within a rectangle. Using the boundaries: 

\(x = 0\)

\(y = 2\)

\(y = 34/7\)

\(x = 24/7\)

The area of this rectangle is \({20\over7} \times {24\over7} = {480\over49}\)

The area of the trapezoid is the area of the rectangle minus both triangles on the sides of the trapezoid.

The first triangle has a height of \(6 \over7\) and a width of \(24 \over7\), making the area \(72 \over49\).

The second triangle has a height of \(20 \over 7\) and a width of \(10 \over 7\), making the area \(100 \over 49\). 

This means that the area of the triangle is: \({480\over49}-{72\over49}-{100\over49}=\color{brown}\boxed{308\over49}\)

Here image: 

I plugged it into a calculator, because I personally can't solve it. Here is what I found:

\(a = {\sqrt{30}\over4} \)

\(b = {2\sqrt{30}\over15}\)

\(c = {\sqrt{15}\over\sqrt2}\)

\(d ={ \sqrt{30}\over5}\)

\(e ={ 2\sqrt{30}\over3}\)

It can't be. If b were 0, then ab would equal 0, not 1. 

Also, don't say that... Constructive Feedback. 

As Melody said, "Learning is a journey..."

Me too lol...

\(3.78^3 = 54.010152\)

\((10^3)^3 = 10^9\)

Move the decimal point to the left 1, and you have : \(5.4010152\)

Because we moved the decimal point back by 1, we add 1 to the power of 10, making the answer: \(\color{brown}\boxed{5.4010152 \times 10^{10}}\)

\(\sqrt{400} = 20\)

Every number from 1 - 400, so \(\color{brown}\boxed{400}\) integers

\(1 - ({1 \over3}+{1\over4}+{1 \over4})\)

This equation leads you to the answer. If you still can't find it, use a calculator and evaluate the expression. 

To get the percentage, multiply your answer by 100. 

For the third question, they should give up swimming. 

The perimeter of the shaded region is  \(10+\text{arc}(QP)\). The circumference of the entire circle is \(10\pi\). The arc is \(1 \over 6\) of the total perimeter, meaning that the arc's length is \({5 \over 3}\pi\). Thus, the perimeter is \(\color{brown}\boxed{10+{5 \over3}\pi}\)

Write is as an equation, where \(x\) is the cost per year: 

\(1.21x=1.3(x-10,000)\)

\(1.21x=1.3x-13,000\)

\(-0.09x=-13,000\)

\(0.09x=13,000\)

\(\color{brown}\boxed{144,444 {5 \over 9}}\)

A very expensive state college indeed :)