Does the graph look like this:
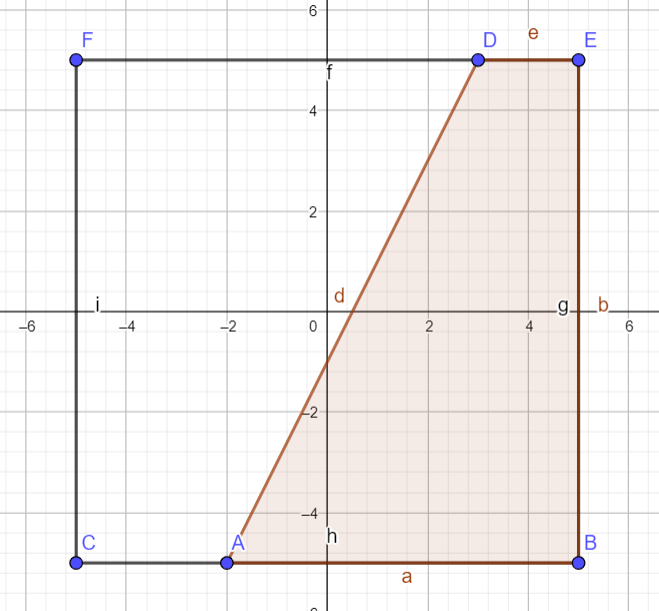
Treat the sign as an equal sign for now (we'll worry about it later)
Start by finding the equation in slope-intercept form(\(y = mx + b\)), which can be done with the slope and y-intercept.
The slope from \((x_1, y_1)\) to \((x_2, y_2)\) is \({\text{rise} \over \text{run}} = {y_2 - y_1 \over x_2 - x_1} = {5 - -5 \over 3 - -2} = {10 \over 5} = 2\)
Now, plugging this into m in the slope-intercept equation gives us \(y = 2x + b\)
Next, we need to plug in 1 of the points given to us and solve for b: \(5 = 2 \times 3 + b\), meaning \(b = -1\).
This means that the equation is \(y = 2x - 1\)
Now, simplify as follows:
\(y + 1 = 2x\)
\(y - 2x + 1 = 0\)
\(\color{brown}\boxed{y - 2x + 1 > 0}\)
.