Melody

This one is also answered now :)

Thanks very much guest.  

ok I'll do the proof in full

Consider minor arc LB

This subtends the angle LRB at the circumference.  And subtends angle LNB at the centre

So     < LNB= 2*< LRB

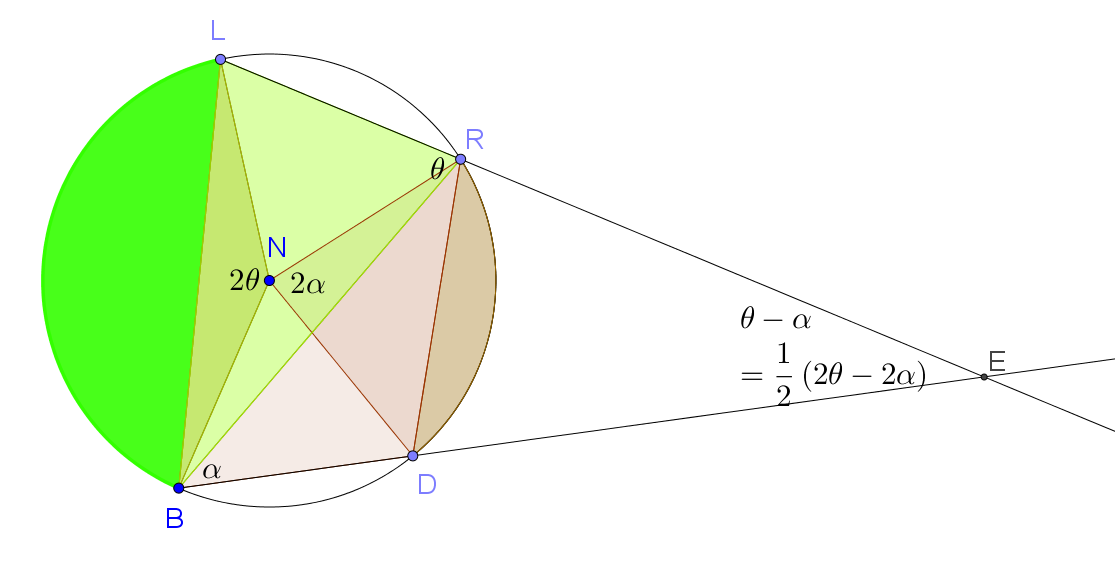
 \(Let \quad \angle LRB=\theta \qquad so \qquad \angle LNB=2\theta\)

Consider minor arc RD

This subtends the < RBD at the circumference.  And subtends

So    

\(Let \quad \angle RBD=\alpha \qquad so \qquad \angle RND=2\alpha\)

\(Consider\quad \triangle RBE\\ \angle LRB=\angle RBE+\angle REB \qquad \text{(Exterior angle of a triangle = sum of opposite interior angles)}\\ \theta=\alpha+\angle REB\\ \angle REB=\theta-\alpha\\ \angle REB=\frac{1}{2} (2\theta-2\alpha)\\ \angle REB=\frac{1}{2} (\angle LNB-\angle RND)\\ \)

-15 +(30 + 18+ ....... )

-15+( sum of a GP with a=30, r=0.6 n=10)

\(-15+\frac{a(1-r^n)}{1-r}\\ =-15+\frac{30*(1-0.6^{10})}{1-0.6}\\ =-15+\frac{30*(1-0.6^{10})}{0.4}\\\)

-15+(30*(1-0.6^10))/0.4 = 59.5465 m

This is to the 10th bounce but it does not include the 10th bounce

Feel free to ask questions :)

Thanks guest 

That is what I thought too but I don't like the terminology much.

What was wrong with how we did it in the old days. Lol

I still don't know how to answer the question though :((

1.56*sin45=1.33sin(theta)

\(1.56*sin45=1.33sin(\theta)\\ 1.56*\frac{1}{\sqrt2}=1.33sin(\theta)\\ 1.56*\frac{1}{\sqrt2}\div 1.33=sin(\theta)\\ sin(\theta)=0.829388405\\ \theta=sin^{-1}0.829388405\\ \theta \approx 56^\circ 2'9'' \qquad \text{This is just the first quad answer}\\ \text{Sin is positive in the second quad as well}\\ \theta \approx 180^\circ-56^\circ 2'9''\\ \theta \approx 123^\circ 57'51''\\ so\\ \theta \approx 56^\circ 2'9''+2n\pi \quad or \quad \theta \approx 123^\circ 57'51''+2n\pi \quad where\;\; n\in Z\\ \text{Put that together and you get}\\ \theta =180n+(-1)^n*56^\circ 2'9'' \quad where\;\; n\in Z\\ \)

You mean average increase per year. ??

Do you have a question with numbers ??

There are 360 degrees in a circle and the area of a whole circle is  \(\pi*r^2\)

so

are of a sector is the fraction of the circle that you have.  

 i.e.      \(\frac{sector\; angle \; }{360}\)

multiplied by the are of the whole circle.

------

which is

\(\text{Area of sector }=\frac{sector\;angle\;in\;degrees}{360}\times \pi r^2 \qquad units^2 \)

you could have told us what you got so if we thought it was wrong we could have discussed it  :)

No the formula for compound interest is 

\(FV=PV(1+r)^n\)

where

FV=future value

PV = present value (at the start)

r is the rate per compouning period expressed as a decimal

n is the number of compouning perods.

so 

If you inbest $250 for 3 years at 6% per annum compounded monthly then

n = 3*12 = 36   (months)

r=  0.06/12 = 0.005   ( this is the rate per month)

so

FV(in three years) = \(250(1+0.005)^{36} = 250*1.005^{36} \)

250*1.005^36 = $299.1701

There is no D on the pic. 

Is D and O the same perhaps?

Also what does "measure arc LB" mean ? is it an angle or an arc length?

What does m