Melody

Thanks Heureka and guest,

I think my logic is similar to guests but I did not really understand guest's that well.

Here is my diagram.

1) On my diagram I have labeled the angles of the triangle ABC

2) Then using only the fact that corresponding angles on parallel lines are congruent, I have labelled all the relevant angles in black.

3) Now, using the fact that the angle sum of a triangle is always the same (180 degrees but that does not matter) I have filled in the 3rd angle on all of the triangles - they are in pink.

4) Now it can be seen that there are 4 similar triangles. (3 equal angles test)

  Also there are 3 parallelograms.  

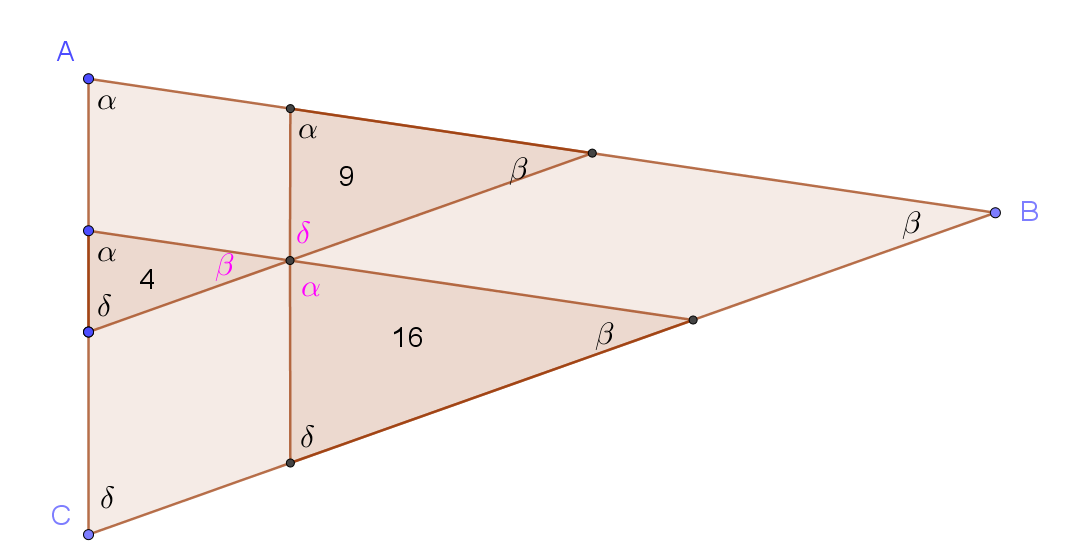
5) Now the ratio of the areas of the 3 small similar triangles is                    4:9:16

6) so the ratio of corresponding sides of the 3 small similar triangles is       2:3:4

7) On the next diagram I will label 3 coresponding sides with their lengths   (in black)

8) Then I will use the fact that parallelograms have opposite sides of equal length to fill in the missint length secions on AC (in red)

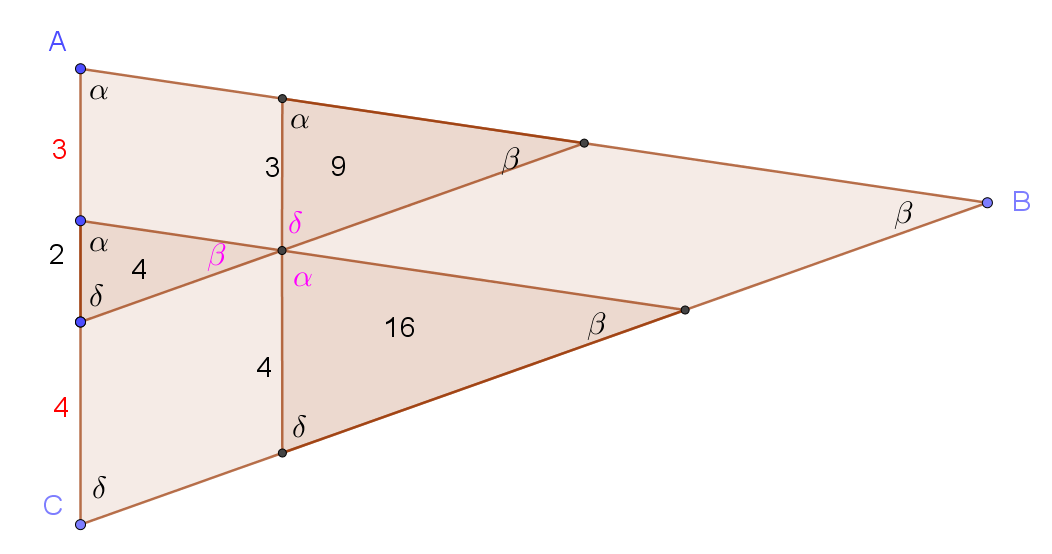
9)   3+2+4=9

10)   So now I know that the ratio of the coresponding sides of the 4 similar triangles is    2:3:4:9

11) So the ratio of the areas of the 4 similar triangles is                                                      4:9:16:81

Since the areas of the little ones are exactly 4,9 and 16, the area of the big one, i.e. triangle ABC is 81 units squared.

I think it is only 10 ways.

Put the teal bead on first. It is the marker bead. This takes care of the rotation aspect.

Then you have 2 lots of 3 identical beads. so that is 6!/(3!3!) ways to place them. Which is 20 ways.

But the braclet can be flipped so I think this will halve the number of possibilities

For instance  TOOOBBB is the same as TBBBOOO

So I think the answer is 10 ways.

It has a negative leading coefficient becaus on the right hand side it ends down not up.

The degree must be even because the left side is down too   

It is not a parabola so there is probably a triple root at x=0. 

This is not a technical explanation it is just one that I hope you can learn from.

\(y=-x^3(x+2)\)

That is a lot of work from both of you. Thanks Chris and XSquaredFactor.

That is some impressive LaTex too XSquared . 

Good work guest. It is good to see you trying to work this out.

It would be good if you becamse a member becasue then it is more freindly and there are other little perks as well. 

((2*3)*5)*67 = 2010

The prime factors of 2010 are 2,3,5 and 67

A fraction will only terminate if the prime factors of the denominator are powers of 2, 5 or 10.

  \(\text{So for }1 \leq n \leq 2010\\ \frac{n^2}{2010}\)

will TERMINATE only if  the 3 and the 67 can cancel out with a 3 and a 67 in the numerator.

3*67=210

2010/201=10

Only 10 will terminate.

So 2000 will not terminate.

I am really not sure what the qustion is asking.

There are 3 unknowns,  x,y and z so how cha you have sloution pairs?

Here is my take.

\(x+2y+2z=n\\ x+2(y+z)=n\\ \text{Let } \color{red}Q=y+z\\ x+2Q=n\\ \)

Now i will solve for integer values of x+Q

I can see that  -1+2=1

so  1(-n)+2(n)=n

If k is an integer then

1(-n+2k)+2(n-k)=n

If x and Q are both positive integers then

\(-n+2k\ge1 \qquad and \qquad n-k\ge1\\ 2k\ge1+n \qquad and \qquad -k\ge1-n\\ k\ge \frac{1+n}{2} \qquad and \qquad k\le n-1\\ \frac{1+n}{2} \le k\qquad and \qquad k\le n-1\\ \frac{1+n}{2} \le k\le n-1\\ \text{Now I want 28 different possible integer values of k so }\\ n-1-\frac{1+n}{2}+1=28\\ n-\frac{1+n}{2}=28\\ \frac{2n-1-n}{2}=28\\ n-1=56\\ n=57 \)

But of course I have made up my own question because yours does not make sense to me.

If n=57 then there are  28 soltions for x an Q      [Not for x y and z]

You are both doing better than me.

I have absolutely no idea what is being asked   

Thanks guest. 1 is not a prime number but that is not central to your arguement.

I am afraid your second paragraph makes no sense to me at all.

Thanks for you input though :)

4x- (x+8) 

there are many ways that you can think of this but the answer will always be the same.

Consider 

10 - (3+5)

the answer is 10-8 = 2

which is the same as   10 - 3 - 5 = 2

so

4x - (8+x) = 4x - 8 -x     =  3x-8

OR

If there is a minus sign in front of a bracket you can get rid of the bracket and the minus sign by changing the sign of everything within th bracket. Minus signs become + and plus becomes -

4x - (8+x)

=4x - (+8+x)

=4x    -8-x

=3x-8

OR

Another way I like to look at it is that you are adding -1 times the bracket

so

4x - (x+8)

=4x+     (-1)(x+8)

=4x+        -1*x + -1*8

=4x+           -x   -   8

=3x - 8 

\(AB^2=25+16-40cos(180-\theta)\\ AB^2=41+40cos \theta\\ AC^2=41-40cos\theta\\ AB^2+AC^2=82\\ M=m=82\\ M-m=0 \)