Melody

That is excellent, if what you say is completely true then you understand, and have memorised, a lot of things now.

Use desmos to look at these 2 graphs, also paste the grapns in your answer (both on the same graph)

y=sinx

y=sin(2x)

What features are the same, what features are different.  What effect does the 2 in front of the x have?

Calamitous Clod rolls a pair of rigged dice. The probability of rolling k on a die is directly proportional to k. 

What is the probability that the sum of Calamitous Clod's dice is equal to 7?

Mmmm.  Am I supposed to assume that these are 6 sided dice?

Prob(rolling1) = k     Where k is less than 1

Prob(rolling 2) = 2k

P(3) = 3k

..

P(6)=6k

k(1+2+3+4+5+6)=21k

21k=1  so

\(k=\frac{1}{21}\)

\(P(throwing 7) \\ = 2[P(1,6)+P(2,5)+P(3,4)]\\ =2[  k*6k  + 2k*5k + 3k*4k]\\ =2k^2 (6+10+12)\\ =56k^2\\ =\frac{56}{441}\\ =\frac{8}{63}\)

You need to check what I have done. 

It has been pointed out to me that k is the number on the die. I should have used a different letter for the proportionality constant.

If you change all my k's to a different letter, it would be a much better answer      

ok, maybe you will learn.  

Your appology is appreciated.

That is great. 

Have you realised that the crest (top) will be the midline + the amplitude   [the y value I mean]

And  that the trough (bottom) will be the midline  - the amplitude

I hope you knew, or worked out those answers BEFORE you actually graphed them. 

I like that you graphed the midline too :)

Ok,

1) Tell me the features of

y=-cosx-2

2) graph it by hand

3) Check it afterwards.

--------------------------------

I almost never look at questions with unnecessary $ signs. It shows me how lazy the asker is. 

Hi answering guest,

I think that you have double counted.

lets assume there are 2 prizes. Non americans get both.  there would be 11 ways for the first one to be allocated and 10 ways for the second one.

So that is 110 ways to place the non americans in realtion to EACH OTHER

Now the american has to be slotted in.  There is 4 to choose from and 3 places to chose from (infront, in middle, or at back)

So that is 12 ways the americans can be slotted in

Altogether I think there are    110*12 = 1320 ways.

Here is the graph of y=1/x

You can see that as x approaches 0 from the positive side, 1/x approaches infinity.

But

you can also see that as x approaches 0 from the negative side 1/x approaches -infinity.

Therefore  1/0  is undefined.   

Yes that is all correct.

Yes can you see that if you move the sinx curve  pi/2 radians (90degrees) in the negative direction that it will be EXACTLY the same as the other curve?

The parent curve that you have been working on so far is    y=sinx     

                             It passes through (0,0) on it way up.    The x axis is its centre line.

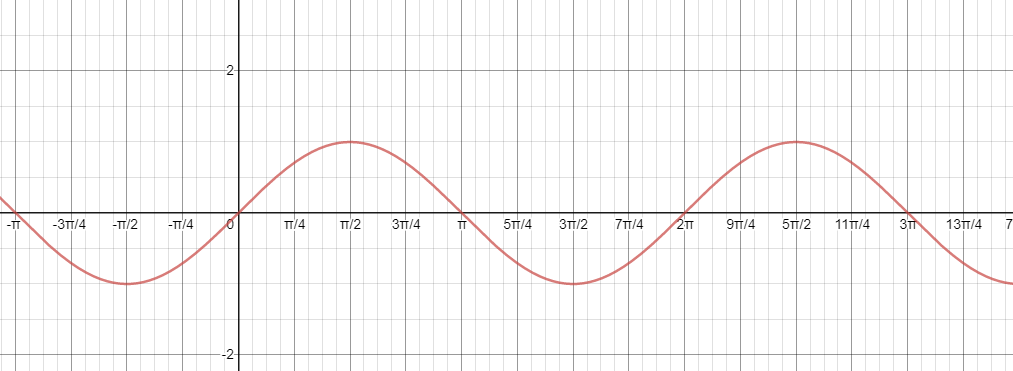
The new curve (which will be a different parent curve)    is    y=cosx.   

                            It passes through (0,1) which is at the very top of the wave.  The x axis is its centre line too.

                            You must memorise these two curves.

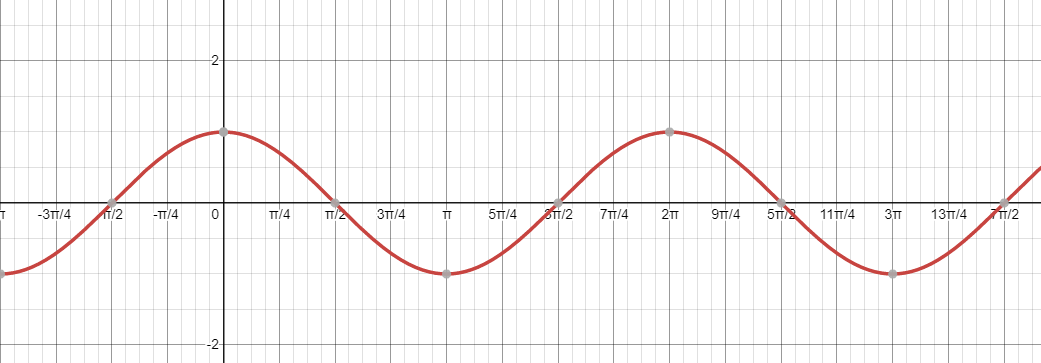
The equation of the cosine curve behaves the same as the sine curve.

Fill out this table and hand graph each one seperately as you do so.

eg

NOW you have your hand sketches, check them with desmos.

30 minutes when travelling at S-4  miles per hour

20 mniutes when travelling S+4 miles per hour

Speed = distance /time

speed * time = distance

so

distance = 20(S+4)=30(S-4)

Now I am up to where guest started :)