Melody

How many integers n between 1 and 10,000 are there such that $7/n$ is a terminating decimal?

I found this easily in google:

"To find out whether a fraction will have a terminating or recurring decimal, look at the prime factors of the denominator when the fraction is in its most simple form. If they are made up of 2s and/or 5s, the decimal will terminate."

So that means that  the desired numbers must be of the form 

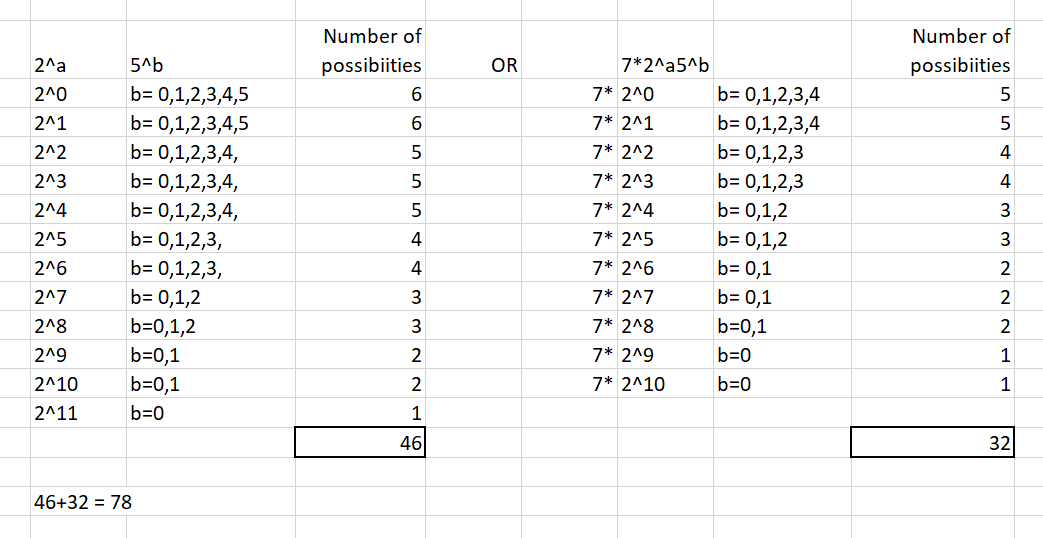
 \(2^a*5^b\qquad or \qquad 7*2^a*5^b\)

where a and b are integers greater or equal to 0

I just used excel to help me organize the possibilities.

I also got 78 possibilities

pi / 64

\(\frac{\pi}{4}\div 16 = \frac{\pi}{64}\)

count the  multiples of 8.   (how many are there)

Then put that over 100   (which is the total number numbers.)

Solve |4y + 1| < |2y - 3| - 7

4y+1>=0   when  y>= -1/4   = -0.25

2y-3>=0 when   y>= 1.5

so you have three regions you must solve for

y< -0.25                     -0.25 <= y <  1.5        and       y>=1.25

set up the correct equation (without absolute signs)  for each of those and solve them.

1 will divide any so that is 5 pairs

2 divides 4 and 6 so there is 2 pairs

3 divides 6 so that is 1 pair

so 8 pairs are favourable

there are  6C2 = 15 pairs altogether

so   P(little one divides the larger one) is  8/15

Yes, that is true.    

deleted.   

First draw a pic

2) find (theta)         Use cosine rule         

3) 2 times the area of the triangle.     

Bingo.

Here is a good start.

From your desctiption there are 2 possible point T's 

See if you can work out what i have done and finish it for yourself.

Maria has three identical apples and three identical oranges. How many ways are there for her to distribute the fruits among her four friends if she doesn't give Jacky any oranges? (Note: Maria takes none of the fruit herself, and some of her friends might not receive any fruit at all.)

I have used what is called the 'Stars and Bars' method.

I get 200 ways

put the 3 apples in a row, they are the stars.  Use bars to divide them into 4 piles, you will need 3 bars

So you have 3 apples and 3 bars so there are  6C3 places to put the bars = 20 possible ways to distribute the apples

now put the 3 oranges in a row (the new stars) Us bars to divide them into  3 piles, you will need 2 bars.

So you have 5C2 = 10 ways to distribute them

20*10 = 200 ways