Melody

They are the only ones I can think of too.

I got down to

\(a^2+b^2 -ab=1\)

Not sure how to determine if those are the only 4 answers.

Attn:  sofsicle

A response from you would be appreciated.

How many positive integers N from 1 to 5000 satisfy the N is congruent to 11 modulo 27?

5000/27=185 and a bit

185*27+11=5006  too big

184*27+11=4979

So there are 184 of them

In my experience, this is a very unusual question and I found it difficult.

Five obvious points on the f(a)=b graph are  

(-4,4)    (-1,0)   (0,2)   (2,-1)   (4,-4)

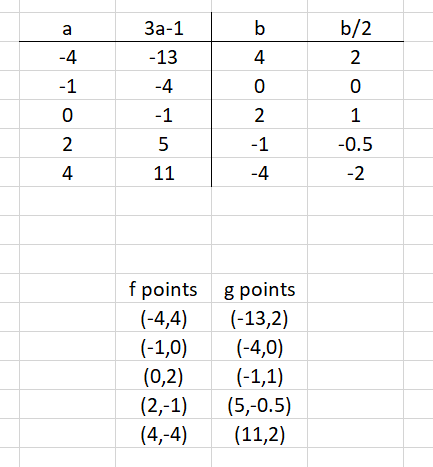
I have graphed these points and the new g function is in red.  

I am not sure what the correct notation is to name it....

Now

\(f(a)=b\qquad g(3a+1)=\frac{b}{2}\\ g(3a-1)=\frac{b}{2}\\ g(3a-1)=\frac{f(a)}{2}\\ let\;\;\;x=3a-1\\ then\;\;\; a=\frac{x+1}{3}\\~\\ g(x)=\displaystyle \frac{f(\frac{x+1}{3})}{2} \)

Check

\(If \;\;x=-4 \;\;then\;\; g(-4)=\frac{f(-1)}{2}=0\quad true\\ If \;\;x=-1 \;\;then\;\; g(-1)=\frac{f(0)}{2}=\frac{2}{2}=1\quad true\\ etc\)

I do not know about describing the transformation.  That is all I have for now. 

If you get an answer or work out how to add to this, please share it with me and with others that may also be interested.

LaTex:

f(a)=b\qquad g(3a+1)=\frac{b}{2}\\
g(3a-1)=\frac{b}{2}\\
g(3a-1)=\frac{f(a)}{2}\\
let\;\;\;x=3a-1\\
then\;\;\; a=\frac{x+1}{3}\\~\\
g(x)=\frac{f(\frac{x+1}{3})}{2}

Well

one of the factors will be   \(x-(1-\sqrt2) = x-1+\sqrt2 \)

think of this as (x-1)+sqrt2

If you introduce another factor as   \((x-1)-\sqrt2\)

Then a factor will be

\([(x-1)-\sqrt2][(x-1)+\sqrt2]\\ =(x-1)^2-(\sqrt2)^2\\ =x^2-2x+1-2\\ =x^2-2x-1\)

now do something similar with the  \(x=2+\sqrt7 \)   root

two questions for you.

1)  When you add these what do you get?

2) What does degree mean?

2022^2021+2019^2020      can you say the last digit

Only considering the last digits

2^1=2

2^2=4

2^3=8

2^4=*6

2^5=*2

2^6=*4

2^7=2^3=*8

2^8=2^4=*6

2^9=2^(5+4)=2^5=*2

so

I need to put  2021 =   1+ 4*505

So the last digit of  2022^2021 will be 2

-------------------------

Now look at powers of 9

9^1=9

9^2=81

9^3=729

9^4 = 6561

9^(1+2n)= **9

9^(2+2n)=**1

9^2020=9^(2*1010)   the last digit will be 1

---------------------

2022^2021+2019^2020  the last digit will be  2+1=3

You need to check what I have done.

Вам нужно проверить, что я сделал

Let

f(x) = 12 - 2x if x <= 4

f(x) = ax + b if x > 4

The function f has the property that f(f(x)) = x for all x. What is a + b?

I started by drawing the g part I know:

I can see from this that if x<4 then  f(x)>4

f(0)=12-0=12

f(12)=12a+b=0

12a+b=0   (1)

f(1)=12-2=10

f(10)=10a+b=1

10a+b=1 (2)

Solve (1) and (2)  simultaneously and you get a=-0.5  and b=6

I checked this answer and it worked fine.

The answer will be a multiple of 5 if one, or both, of the numbers ends in 0 or 5.

There are 90 numbers in total and 18 of them end in 0 or 5

The prob that the first one is a multiple of 5 and the second one is not is   \(\frac{18}{90}*\frac{72}{89}=\frac{72}{445}\)

The prob that the first one is not a multiple of 5 and the second one is will be the same    72/445

The prob that they are both multiples of 5 is   \(\frac{18}{90}*\frac{17}{89}=\frac{17}{445}\)

P(that the multiple will be a multiple of 5) = \(\frac{2*72+17}{445}=\frac{161}{445}\)  

You need to check for careless errors.

Draw it up on a grid and then use Pythagoras's theorem to find the hypotenuse.

The times the answer by 0.25

The answer is in miles