+118703 
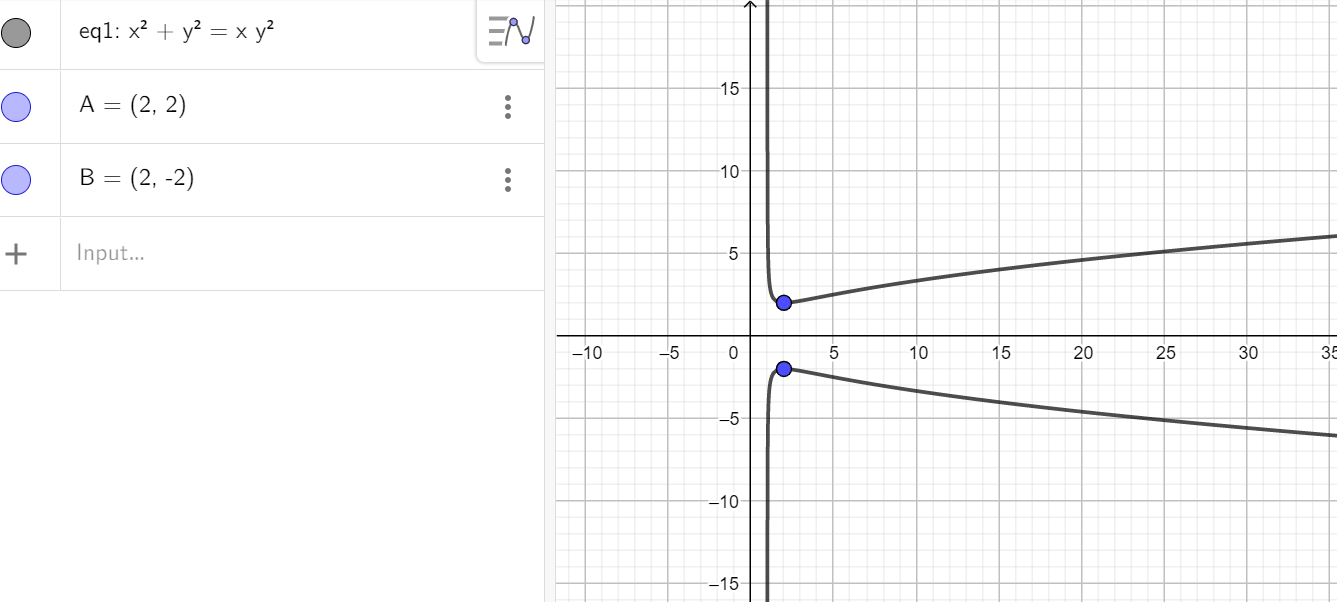
+118703 Fist thing I did was graph it.
https://www.geogebra.org/classic/svfrstbf
a^2+b^2=ab^2
its symetrical so I want to look at the top half b>0 (then I will double the number of answers)
\(a^2=ab^2-b^2\\ a^2=b^2(a-1)\\ b=\frac{a}{\sqrt{a-1}} \)
a has to be greater than 1,
For b to be an integer
a^2 = k (a-1) where k is an integer
---------------------------------
yea I don't know.
There are at least 2 answers.
+118703 Thanks for your answer Heureka,
This answer has since been questioned here https://web2.0calc.com/questions/advanced-quadratics-help-pls
so I took a look at what you have done.
The only oversight i can see is that since p and q are positive, pq must also be positive
so pq = 2+sqrt(53)
which means that a+b+c+d =161
