CPhill

log₂ x  = 10

Exponential  form :

2¹⁰  = x

b  = 2

x = x

n = 10

A)  The area  is just  (4x - 7)  (4x - 7)  =  16x^2 - 56x  + 49

B)  We have a polynomial of degree 2   (a quadratic)

C)  Polynomials are "closed"  under multiplication because  any two (or more) polynomials multiplied together always produces another polynomial

("Closure"  means that any operation(s) done on like objects always produces another like object  )

Remember Manuel....that

log a^b  =  b log a

So

log x⁵  =   5 log x

Hey, Haley  !!!...I think this is what you have

[26 (-1)]  - [(-5) (-2)]

_______________  =

3 *  [ 24 / (-3-3) ]

[-26]  - (10)

__________    =

 3  [ 24 / -6 ]

    -36                -36

______   =       _____    =         3         (  LOL !!!!  )

 3 [ -4 ]               -12

We can use some symmetry here....this pic might help :

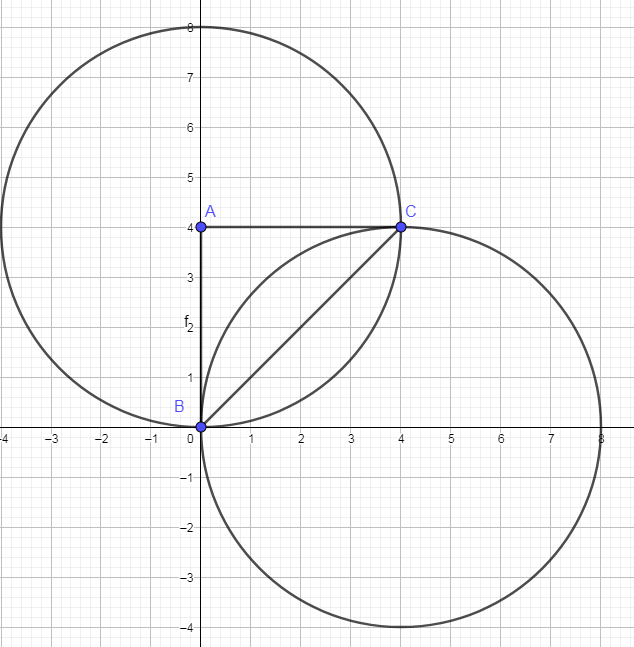
Locate the center of the top circle  and draw two radial lines to each end of the shaded figure in ths circle

Let the center of the circle be  A....let  one of the radial lines intersect the "bottom" of the shaded area in this circle at B  and Let the other radial line intersect the other end of the shaded area in this circle at  C

Connect BC....and this will divide the shaded area in two equal parts

Now we can take the circle sector ABC  as the quarter area of this circle.....its area will be  (1/4)pi(4^2)  = 4pi   (1)

And we can take the area of triangle ABC  as   (1/2) (4^2) sin(90°)  = 8   (2)

Now the difference in (1)  - (2)  will give us half of this shaded area  =

(4pi - 8) units ^2  =  4 (pi  - 2) units^2

So...the whole shaded area in one circle is twice this  =  2 * 4 (pi  - 2) units^2  =  8(pi  - 2) units^2

And since we have 4 of these areas - one in each circle -   the total of the shaded areas  is  just

4* 8(pi  - 2) units^2    =    32 (pi  - 2) units^2   

Let's look at this one closely......

Here's a pic :

We have  altitude  BC  drawn to a right angle in  triangle ABD

Note that triangle ABC  is similar to triangle CBD

Thus

AB / BC  = CB / BD     which implies that

4 / BC  = BC / 9        cross-multiply

36  = BC^2       take the square root of both sides

6  = BC  = "y"

Thus,  altitide BC in  this situation serves as a geometric mean to the two bases of each of the smaller triangles formed

Happy Birthday, CowGirlKatie.....!!!!

3. Find an equation that models the hyperbolic path of a spacecraft around a planet if a=107124 km and c=213125.9 km

Let's let the center be (0,0)  and let  the hyperbola intrcept the y axis

The form is

y^2     -    x^2

___        ____    =    1

a^2         b^2

a = 107124

c = 213125.9

So

b^2  = [213125.9^2  - 107124^2]    .....this is a huge number...let's just leave it as this

So.....the equation is

    y^2             -             x ^2

 ________           ____________________   =     1

 107124^2          [213125.9^2  - 107124^2 ]

2. foci (0, +or- 25) vertices (0, +or- 7)

This hyperbola intercepts the y  axis and is centered at (0,0)

The form is

y^2     -  x^2

___       ___    = 1

a^2        b^2

a  = 7

c  = 25

b = √[ 25^2  - 7^2 ]  = √  [625 - 49 ]  =√576  =  24

So.....the equation is :

y^2   -    x^2

___       ___     = 1

49         576

Here's a graph  :   https://www.desmos.com/calculator/fyyifnyzze

1. foci (+or- 17, 0) vertices (+or- 8, 0)

This hyperbola  will  intercept the x axis  and be centered at (0,0)....so it will have the form

 x^2            y^2

 ___   -      ___      =  1

 a^2           b^2

a = 8

c  = 17

b  =√ [ 17^2  - 8^2]  = √ [289 - 64]  = √ 225  =  15

So....the equation becomes

x^2        -     y^2

___            ____   =  1

64              225

Here's a graph :  https://www.desmos.com/calculator/a2uusijq3k