CPhill

2.

\(y=\frac{x-2}{x^2-7x+10}\)

Factor the denominator

y =        (x - 2)

     ___________    

       (x - 2) (x - 5)

This will not be defined  for any values that make the denominator  0

Thus....it will not be defined when x  = 2   or  x = 5

Thus.....two values

It's been awhile since I did this...so...here goes nothing

v = (3, 4)     w  =  (-2, 7)

We want to project  v onto w

proj_w v  =   [( v dot w) /( length of w)^2 ] * w  =  [ 22/ 53) * (-2, 7)  =  (-44/53, 154/53)

This  is   v1

To  find v2   we have    [ v - v1] =  (3, 4) - (-44/53, 154/53)  =  (203/53, 58/33)

Here's a pic :

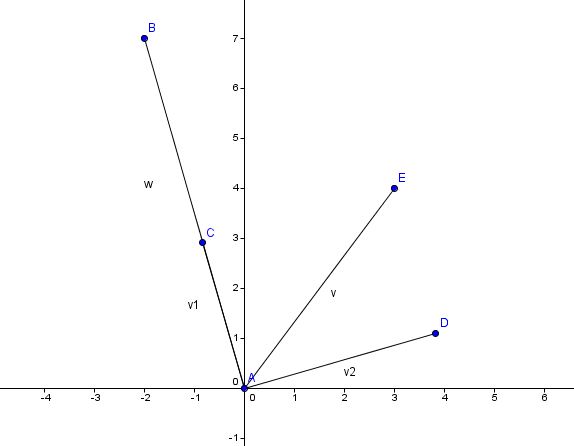
The "why" of this always gave me some trouble, too. If I can remember what my  Calc teacher said, if we shine a beam onto v from the "top" of the diagram perpendicular to v2, it will "project" a perfect "shadow" of v onto v2. Likewise....if we shine a beam from the "right" of the diagram onto v such that the beam is perpedicular to v1, it will "project" a perfect "shadow" of v onto v1.

Sorry, hectictar.....that's about as good of an explanation as I can supply......!!!!

I think this is used in Physics to break up components of work  (as well as some other applications, too...)

Here's my best effort  ....

If the perimeter of the rectangle is 26....then 

2(W + L )  = 26

W + L  = 13

Then  L  =  13 - W

Call point Q  =   ( W , L )  =  (W , 13 - W)

So.....using the equation of a circle with a center O located at  (0,0)  and a radius of 10, we have

W^2  + (13 - W)^2  =  100

W^2 + W^2 - 26W + 169  = 100

2W^2 - 26W + 69  =  0

Solving this for W  we get that W  =  [ 13 + √31] / 2  = OP

And L  =   [ 13  - √31 ] / 2  = PQ 

So  PR  =  (1/2) √ [  ( 13 + √31)^2 + (13 - √13)^2 ] =  (1/2) √[ 382 + 26√31 - 26√13 ]

So.... the perimeter  =

arc BQA  + AP  + PR  + BR  =

5pi + (10 - OP) + PR + (10 - PQ)  =

5pi  + (10 -  [ 13 + √31] / 2 )  + (1/2) √[ 382 + 26√31 - 26√13 ]  + (10 -  [ 13  - √31 ] / 2 )  ≈

33.1125  units

Look at the graph, here :   https://www.desmos.com/calculator/jegh0wzpku

a. The max value  is  60    ....the  min value is  -4

b. It is at a max at 11 AM

c.  The index  is above 48  from 7.579 hours after midnight to 14.421 hours after midnight  (this trasnlates to  about  7:35AM to about 2:25 PM )

d.   The amplitude - the "32" -  will be affected ...it will be 90% of its current value  = 32*.9  = 28.8

Thus...the index max will be reduced to  28.8 + 28  = 56.8

e.  The new equation will be   I  = 28.8sin [ 15 (t - 5) ] + 28

f. Look at this graph : https://www.desmos.com/calculator/i04rsjwpbt

The new  legislation  will mean that the index level will be > 48  from about 8PM to about 2PM....thus....it shortens the previous window by about one hour

sec =  r / x   ...so    r  = 6  and  x  = 1

We need to find y......since this angle is in the 4th quadrant, y will be negative

So  y  =  - √  [ r^2 - x^2 ] =  - √[ 6^2 - 1^2 ]  =  - √35

 sin (t)  =  y / r  = -√35 / 6

cos (t)  = x / r  = 1 / 6

tan (t)  =  y / x   =   -√35 / 1  = -√35

csc (t)  = r  / y  =  6 / -√35  =  ( -6/ 35)√35 

cot (t)  =  x / y  = 1 / -√35  =   -1/√35  =  -√35 / 35

OK....I'm out-voted....LOL!!!!!

Very well explained, X² .....!!!!!

sin (x + 21)  = cos (2x + 21)

Since these are cofunctions....the angles add to 90°

So  we have

x + 21  + 2x + 21  = 90     simplify

3x + 42  =  90      subtract 42 from both sides

3x  =  48    divide both sides by 3

x = 16

Second one

The triangle on the left is a 45-45-90 right triangle....the hypotenuse = 2√2

And the other two sides are 1/√2  times the hypotenuse

So the   common side of both triangles  =  2√2 ( 1/√2) =  2

Since  the triangle on the right is a 30-60-90 right triangle, the side opposite the 60° angle, y, is √3  that of the side opposite the 30° angle......and the side opposite the 30° angle  = 2

So...y  = √3 * 2   =     2√3

RainbowPanda has assumed a radius of 3...I assumed a radius of 6......from the pic...I can't actually tell if the "6" is the radius or the diameter.....

Anyway......you have an answer for each assumption  !!!!

Thanks, RP  !!!!

12

The percentage is given by  68 / 83  ≈  .82

13   Order the data      

Group A      32   36   36  37  41  42  44  45

Group B      26   36   36  38  40  40  40  42     

Mean Group A   =   39.125

Mean Group B   =   37.25       so....not true  

Range

Group A  =  45 - 32  =  13

Group B  =  42  - 26  = 16    false

Mode

Group A  = 36

Group B  = 40   false

Median 

Group A  =  [ 37 + 41] / 2  =  78/ 2  =  39

Group B  = [ 38 + 40 ] / 2  = 78 /    = 39    true