CPhill

We have

[ 90  - 100 ]  / 25  =

-10 / 25  =

- 2 / 5  = 

- .4

The   table value for this z score  is  .3446

So

.3446  ( 400)  ≈  138  people

P ( 1 < X  < 5)  =

P(2) + P(3) + P(4)  =

0.07  + 0.22  + 0.22  =

0.51

We have

[ Observed value  - Mean Value  ] / Standard Deviation

[259 - 239]  / 25  =

20  / 25   =   4/ 5  =  .8  

We know  the oppoite side and the adjacent side....the inverse tangent is what we need

arctan ( 26/53)  = 26.1°

Arc  length, S,  is

S = r * theta (in radians)

S  =  21 5/8  *  ( 5 pi / 6)   =   [ 173/8 * 5 /6  * 3.14 ] =   56.59   yds

x^2   - y^2  = 1

(r cos  θ)^2  - (r sin  θ)^2  = 1

r^2 cos^2  θ - r^2 sin^2  θ   =  1

r^2 ( cos^2  θ  - sin^2  θ)  = 1

r^2  (cos 2 θ)  = 1 

x^2  + y^2   = 25

r^2  = 25

r  = 5

See the following ACG :

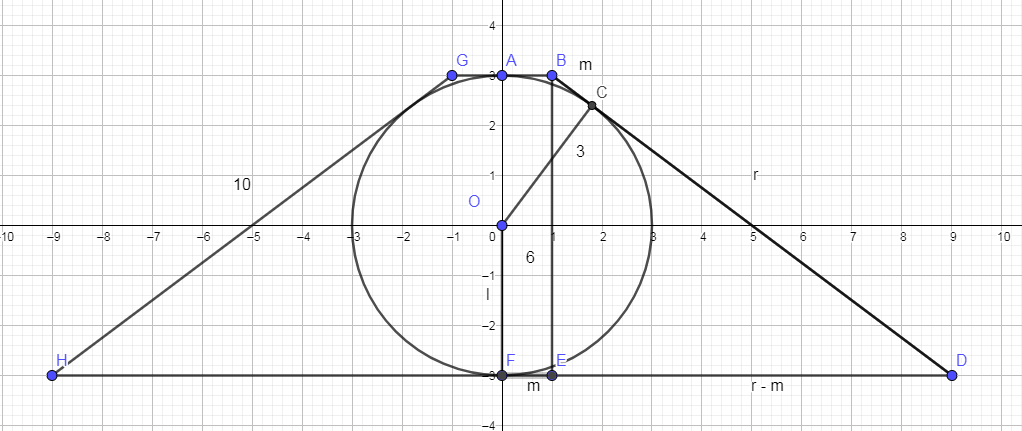
Since the sphere is tangent to  both the top and bottom bases, the height of the frustum must be   = 6  = BE

And the slant height   = 10  = BD

Notice that  since  AB   and BC  are tangents drawn from  the same point, they are equal

And AB  = 1/2 ot the top  base  of the frustum.....so BC  equals the same.... and  call this, m

But  CD  and  DF are also  tangents drawn from the same point.....so CD  = DF

And because  of the Pythagorean Theorem,  DE  = √ [BD^2  - BE^2=  = √[10^2 - 6^2 ]  =   8  =   r  - m

So.....we have the following eqautions

r + m  = 10

r - m  =   8      add these

2r  = 18

r  = 9   =  bottom radius

So...  9 + m  = 10  ⇒ m  = 1   = top radius

So....the  volume of the frustum  is

(1/3)  pi  *  height  * ( top radius^2  + product of the radii + radius ^2 )  =

(1/3) pi  *  6  * ( 1^2  +  1*9   +  9^2 )  =

(1/3) pi * 6 * ( 1 + 9  + 81)  =

(1/3) pi * 6 ( 81)  =

182 pi  units^3

Edited to correct an error  !!!

                                Alternate Interior Angle Theorem

∠ ADB    =  ∠CDF

                                  Angle Angle Similarity Postulate

                  Corresponding Angles Postulate

                  Transitive Property

                  Triangle Proportionality  Theorem

                                 Corresponding Angles Postulate

ΔACE  ~ ΔBCD

                                 Segment Addition Postulate