CPhill

Excellent, Knockout  !!!!

BTW....welcome aboard    !!!!

( 1 + i)^2  =  1 + 2i  + i^2  =  1  + 2i  - 1  = 2i

(1 - i)^2  =  1 - 2i  + i^2  =  1  - 2i  - 1  =  -2i

So

( 1 + i)^2016  - (1 - i)^2016  =

[ (1 + i)^2 ] ^1008  -  [ (1 - i)^2 ]^1008  =

(2i)^1008  - (-2i)^1008  -

(2i)^1008  -  (-2)^1008 * (i)^1008  =           [ (-2)^even power  = 2^even power]

(2i)^1008  -  (2)^1008 * i^1008  =

(2i)^1008  -  (2i)^1008  =

0

This is a right triangle...its area  =  product of the leg lengths  / 2  = 

15 * 8  / 2   =

120  / 2  =

60  units^2   

The  area  also equals

(1/2) CD  *  AB  ...so

(1/2) CD  * 17   =  60

CD  * 17  =  120

CD  = 120/17

So..by AA concruency......triangle ACB  is similar to triangle  ADC

Therefore    AD /DC  = AC / BC

AD  =  (120/17) * 6 / 15   =  64/17

And in triangle ADC.....AC is the hypotenuse  and  AD and DC  are the legs...so its area  =

(1/2)  ( AD) ( DC)   =

(1/2) (64/17) (120/17)  ≈  13.29 units^2   

EP..I actually think that the guest's answer is  somewhat correct.....here's why

lAlthough  it is true that there are only   6 diferent  combinations of numbers....sequencing is important....for instance

If the correct combination  is   5  4  1   3   6

This isn't the same as   1  3  4  5  6

So...for each combo....we can  permute them in   5! ways

So.....  6  * 5!   =   720

But only one of the selected sequences must be the correct one

So.....  1/ 720   seems to be the  correct answer   ???

The total number of possible  combinations  = C(6, 5)   =  6

So...the probabilty  is    1 /  6

We can find the area of this triangle using Heron's Formula

s  = [ 10 + 17 + 21  ] / 2  =  48 / 2  = 24

The area  =  √ [ s (s - 10) (s - 17) (s - 21) ]  =  

√ [ 24 (14) (7) (3) ] =

√7056   = 84  units^2

The area   =  1/2  [ sum of triangle's sides ]  *  altitude of each triangle

But....the altitude of each triangle  = the radius  of the incircle

So...we have

84  = (1/2) (48) * radius of incircle

84  = 24 * radius of incircle

84 / 24  = rasius of incircle  = 3.5 units

EDIT TO CORRECT AN ERROR  !!!!

triangle AQB is similar to triangle ZQY

Since  QY  = 24  and BQ  = 12

And   QY + BQ   = 36  = BY

Then   QY  = (2/3)  BY

So... QZ  = (2/3)  AZ   = (2/3) 42  = 28

Thanks, tertre

If tertre's answer is supposed to be in scientific notation....we have  6.3 x 10³

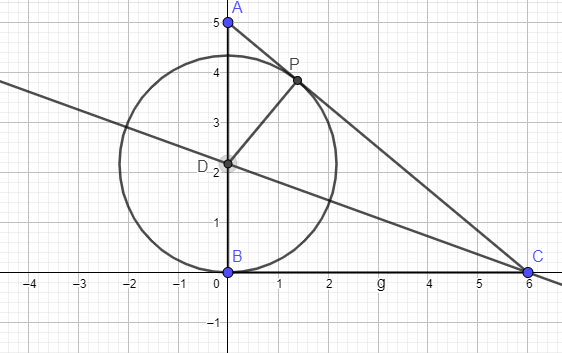
BC  = √ [ AC^2  - AB^2 ] = √ [ 61  - 25 ] = √36  =  6

If the center of the circle  is on AB  and is tangent to BC, then  it is tangent to BC at B

And this tangent  drawn from C  = 6  = BC

But CP  is also a tangent to the circle drawn from C.....and if P is also tangent to the circle...then P's distance from C must be the same length as  BC  = 6

So  CP  = 6

Proof :

Bisect angle BCA....let this bisector intersect AB  at D

This creates two  triangles,  DBC and DPC

angle CPD  = angle DBC  = 90

angle PCD  = angle BCD  [ by angle bisector CD]

CD  = CD

So...by AAS  triangle DBC  = triangle DPC

So....BC  =  PC   = 6

Nice, Omi   !!!!