CPhill

Suppose ABC is a scalene right triangle, and P is the point on hypotenuse AC  such that angle ABP = 45° . Given that AP=1 and CP=2, compute the area of ABC.

Because angle ABP = 45, then the right angle ABC is bisected....this sets up the following relationship in the triangle

AP/CP = AB/BC

1/2  = AB/BC

Let AB = x

So BC = 2x

And AC = 5

So....by the Pythagorean Theorem, 

AB^2 + BC^2  = AC^2

x^2 + (2x)^2  =  5^2

x^2 + 4x^2  = 25

5x^2  =  25

x^2  =  5

x =  sqrt (5)  = AB

2x  = 2sqrt(5)  = BC

So.....the area of ABC =  (1/2)AB * BC  = (1/2)sqrt(5) * 2sqrt (5)  =  5 units^2

I'll do the first.....the second should be easy based on this

3(1) - 1  = 2

3(2) - 1  = 5

3(3) - 1  = 8

3(4) - 1 = 11

3(5) - 1  = 14

Let A = Probability of selecting a black chip with an even number = (1/2)

Let B = Probabilty of selecting a black chip = (3/5)

P ( A  l B )  =   P (A) * P(B)         (1/2) * (3/5)

                      ___________  =  __________ =             1 / 2

                          P(B)                    (3/5)

This makes sense....we already have a black chip in hand.....there is a (1/2) probability that it has an even number

Triangle ABC has AB=BC=5 and AC=6. Let E be the foot of the altitude from B to AC  and let D be the foot of the altitude from A to BC. Compute the area of triangle DEC.

Here's an image :

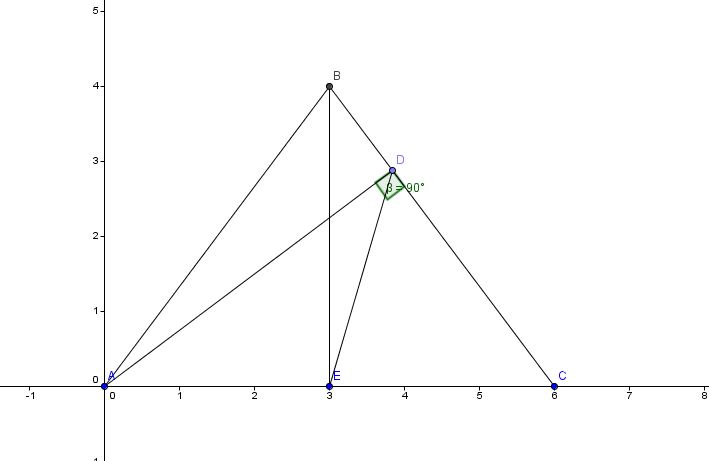
Let A = (0,0)   C = (6,0)

The triangle is isoceles.....so E will bisect AC....so  ....EC = 3

And....triangle AEB is a 3-4-5  right triangle with AE = 3, EB = 4  and AB = 5

So....B = (3,4)

Sine angle BCE = 4/5 = sin DCA = sin DCE

And we can find AD  using the Law of Sines

AD/sin DCA = AC/sin ADC

AD/ (4/5) = 6/sin90

AD = (4/5)6  =  24/5 =  4.8

And...using the Pythagorean Theorem, 

DC =  sqrt (6^2 - 4.8^2 )   = 3.6

And  EC = 3

So....the area of triangle DEC  =

(1/2) (EC) (DC) sin DCE   =

(1/2)(3)(3.6) (4/5)  =

4.32 units^2

Just add these and divide by 2.......that will be your answer

We can use something known as "Pick'sTheorem" to  answer this...

When the vertices of a figure have integer coordinates [ like this one]....the area is given by

(Number of  integer coordinates on  the boundary / 2 ) +( number of interior  points with integer coordinates) - 1 

Number of integer coordinates on the boundary   =  5

Number  of integer coordinates  in the interior = 21

So....the area is

(5/2)  + 21 - 1   =

2.5 + 20  =

22.5 units^2

Mmmmmm...  I liked it.....

Yep....that's the best way to "see" these, I think

There is so much Calculus that I have forgotten......good to get a "refresher"  here...

I agree with Melody.....these ARE confusing....!!!!

Her last graph is pretty good....it will be impossible to create an "exact" graph

Just tried this one for myself.....our answers agree...so....probably correct...!!!