CPhill

No big deal.....all that Christmas food has made my mind hazy, too....LOL!!!!

-16t^2 + 80t + 21

The  t  that maximizes this is given by :

-80 / [ 2 * -16]  =  80 / 32  =  5/2

Putting this back into the function, we get that the max height is

-16(5/2)^2 + 80(5/2) + 21  =

-16(25/4) + 200 + 21  =

-100 + 200 + 21 =

121 ft

k =  (6x + 12) (x - 8)      expand

k =  6x^2 + 12x - 48x - 96     simplify

k = 6x^2  - 36x - 96

The value of x that minimizes k can be found as

- (-36) / [ 2 * 6 ]    =    36  / 12 =  3

Put this back into the function

6(3)^2 - 36 (3) - 96   =

6 * 9 - 108 - 96

54 - 108 - 96  = 

- 150   =  minimum value of k

The value of "a" that minimizes this is given by   --6 / [ 2 * 1 ] =  -/2 = -3

Putting this value back nito the function we get

(-3)^2  + 6(-3) - 7  =

9 - 18 - 7 =

9 - 25  =

-16  =   minimum value

x^2 - 6x + 13

The x value that  minimizes this is given by   - (-6) / [ 2 * 1 ]  =  6 / 2 =  3

Subbing this back into the function, we have

(3)^2 - 6(3) + 13

9 - 18 + 13

22 - 18  =

4   =  the minimum value for the expression

We have this

Last term  =  First Term - 3(N - 1)     where N is the number of terms

39 =  147 - 3(N - 1)      simplfy

39 = 147 - 3N + 3

39 + 150 - 3N       subtract 150 from both sides

-111 = -3N     divide both sides by -3

37 =  N     (37 terms)

Here's one more method :

47 / 5  =  9   Remainder  2

9 / 5  =   1 Remainder  4 

1 / 5 =   0 Remainder  1

Reading the red digits from bottom to top  gives us    142₅

Maybe other ways to do this...but....

The largest that A can be is 1

47 - 1*5^2 =  

47 - 25 = 22

This implies that B = 4  because    4(5) = 20

And C = 2

47₁₀   =   142₅

So

B =  4

Nvm.....see EP's answer below....

Thanks, Melody

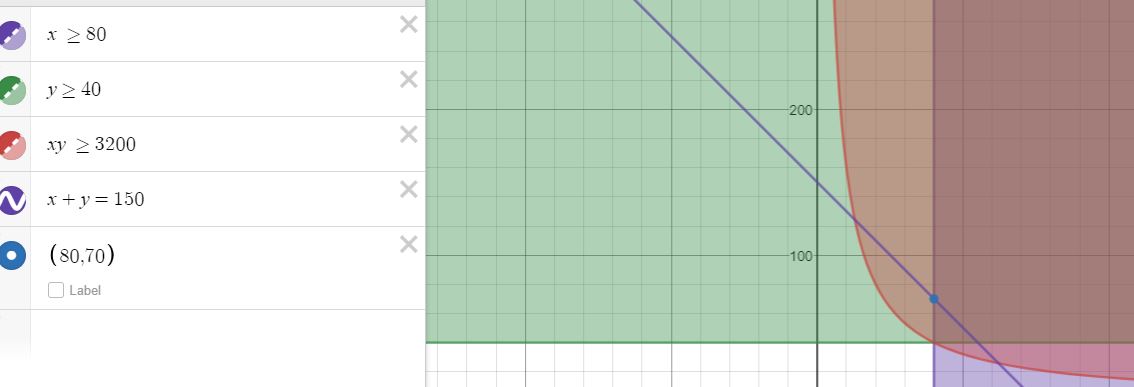
This problem can also be solved by a graphical method

Call x  the width and y the length

We have these constraints

 x ≥ 80

y  ≥ 40

Using these the area, xy,  must be ≥ 3200

And we have the final  constraint that  2x + 2y = 300  ⇒  x + y = 150

The graph shows that the point (80,70) is the  optimum solution....just as Melody found!!!