CPhill

f(2)  = 2^2 - 2(2)  = 0

Note that, from here on,   every  evaluation of the nested functions will  =   0  because f(0) =  0

So

f(f(f(f(f(f(2))))))  =    0

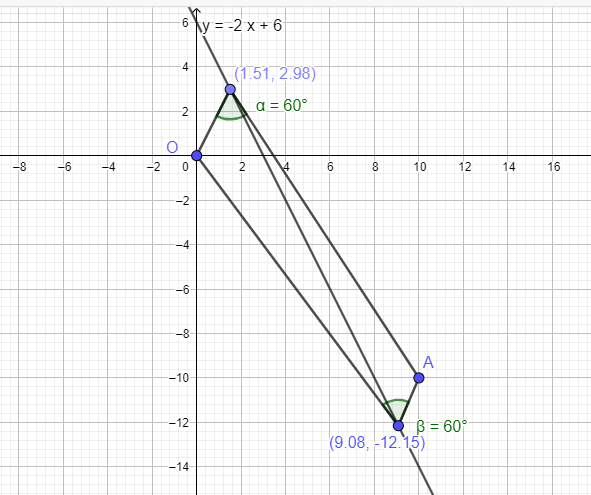
Let the point  Q =  (x , 6 - 2x)

The distance from  O to A   =  sqrt (200)

The distance  from   O to Q =  sqrt  ( x^2 + (6 -2x)^2 )  = sqrt ( 5x^2 -24x + 36)

The distance from  A to Q =  sqrt [ (x -10)^2  + ( 6-2x - - 10)^2 ]  = sqrt [ ( x -10)^2+ (16 - 2x)^2] =

sqrt [ 5x^2 - 84x + 356  ]

Using the Law of Cosines

200 =  (5x^2 - 24x + 36) + ( 5x^2 - 84x + 356)  -2 sqrt [( 5x^2 -24x + 36)(5x^2 - 84x + 356] cos (60)

200 = (10x^2 - 108x + 392) -2 sqrt [ (5x^2 - 24x + 36) ( 5x^2 - 84x + 356)] cos (60)

This is very messy to solve  (as you might expect !!!)  so I used WolframAlpha as a solver

It gives two values

x ≈ 1.5081    so    y   ≈ -2 (1.5081) + 6 = 2.9838

And

x ≈ 9.0758   so    y ≈  -2 (9.0758) + 6  = -12.1516 

Here's a graph :  

So

6 (14)  = 84

And

(84  - x)  /  5 =  5

84  - x  =  5 * 5

84  - 25  = x

59 =  x  =   the number removed

Call  the  one real root , r        The other two roots are 3 + 4i  and 3  -4i

(x - r)  ( x - (3 +4i)) ( x - (3 -4i)   =  0

(x - r)  (x^2 - 6x + 25)  = 0

x^3 - 6x^2 + 25x   

      -  rx^2  + 6rx  - 25 r

___________________

x^3 - (6+r)x^2 + (25 + 6r)  - 25 r =    0

Since  p(0)  = -52

Then   -25r= -52    ⇒  r = 52/25 =  the real root

So

p(x)  =  x^3 - (6+52/25)x^2 + (25 +6*52/25)x - 52         simplify 

p(x)  =   x^3 - (202/25)x^2  + (937/25)x - 52  

P =  (3 /11) ( 2 / 10)  =  6/ 110  =   3 /  55

Rearrange as

x^3  + 6x^2  -  20x  =  0

We have the form  ax^3 + bx^2 + cx + d

Sum of the roots   =  -b/ a  =    -6/1   = -6

1/ (2x)  = (r  - x)  / 5

5  =  2x ( r - x)

5 =  2rx- 2x^2

2x^2 - 2rx + 5

If this has one  real solution  then  the discriminant =  0   .....so.....

(-2r)^2 - 4 (2) ( 5) = 0

4r^2  -  40  =  0

4r^2=   40

r^2  =  10

r = sqrt (10)      or    r  =  -sqrt (10)

Their product =   -10

                                                         28  = N

21   22     23       24       25      26     27

                           25                          26

                           26                          25

                           27                          24

                                                         23

We need to find  the width of the square........ we can   do  this as follows

2x^2 + 6x+ 4  = 7

2x^2 + 6x - 3  =  0

Using the q formula

x = [  -6 + sqrt ( 36 + 24) ]  / [ 2 *2] =    [ -6+ sqrt (60) ] / 4  =  [ -6  + 2sqrt (15) ]  / 4 =  sqrt (15)/2 -3/2

The other  root  is    -sqrt (15) / 2  - 3/2

These two points are where the parabola intersects the line y= 7

So....the width of the  square  =   (-3/2 + sqrt (15)/2)  - ( -3/2 - sqrt (15) / 2)  = 2 sqrt (15)  /2  = sqrt (15)

Area of the square =   (sqrt (15)) ^2  =    15

f ( x)  = 3/ (2 + x)

Write

y = 3 / (2 + x)       get x by itself

y ( 2 + x)  =  3

2y + xy   = 3

xy  =  3 - 2y

x =  (3 - 2y) / y       "swap" x and t

y  = (3 - 2x) / x          this is the inverse  = f^-1(x)

So

g(3)  =  (3 - 2*3) / 3   + 9    =  -3/3 + 9  =     8