CPhill

Note that    sqrt (x^2)  can be defined as   l x l

The range of this  function is  [ 0, inf)

Let the first term  = n

Let the third  =  n + 2d

So

n (n + 2d)  =  9

We have two  different (positive) factors that multiply to 9  →  1  and  9  

So  if   n =  1     and  d = 4   then

1 ( 1 + 8)  = 9

1 (9)  = 9

So the 4th term is    1 + 4(4 -1)  =  1 + 12  =  13

Very nice, Tuffla  !!!

Welcome aboard, Tuffla!!

Here's one  more way

Let him start  at (0,0)

When he walks 800 feet west he is at  (-800, 0)

When he then  walks 900 ft due north he is at  (-800 , 900)

When he then walks 1500 ft due east he is at  ( -800 + 1500, 900) = (700,900)

When he walks due south 100 ft he is at ( 700 , 900 - 100) =  (700, 800)

And his distance from the starting  point (as Tuffla calculated)  is   

sqrt [ 700^2 + 800^2 ]  =

sqrt [ 100^2  ( 7^2 + 8^2) ]  =

100 sqrt [ 113  ]  ft   ≈   1063 ft

Assuming  a box could be empty

Choose all 5 balls to go into  either box  - the other box is empty by default

C(5,5) * 2             =    2 ways

Choose  4 of the 5 balls to go into either box  -  the remaing ball goes into the other box by default

C(5,4)  *2            =    10   ways

Choose 3 of the 5 balls  to go into either box -  the remaining two balls go into  the other box by default

C(5,3) * 2             =   20 ways

32 ways 

The eighth  row of Pascal's Triangle  produces

1   8    28   56  70  56   28   8    1

The only   odd terms will   be  1m^8   and 1n^8  since the multiplication of any product by an even produces an  even

So.....two terms will be odd

45 = (1/2) (height) (2CD + CD)

90  =  (height) ( 3CD)

30  = (height) ( CD)

30  / CD  = height  of trapezoid

AMB  and BMC  are similar triangles

Since  AB = 2CD

Then height of  AMB  = 2 (height of  BMC)

So  there are three equal parts to the height of the trapezoid and  the height of AMB is two of them

So  height AMB    =  (2/3) (30) /( CD)  =  20 / CD

Area of AMB  = (1/2) (AB) [height (AMB) ]    =   (1/2) (2CD) [ 20/CD]  =  20

f(0)  =  a/2

And   we can find  f^-1  as follows

y = a /(x + 2)     get x by itself

y ( x + 2)  = a

yx + 2y   = a

yx  =  a  - 2y

x =  (a - 2y) / y         swap x, y

y = (a - 2x) / x  = f^-1 (x)

f^-1(8a)  =   (a - 2(8a)) / (8a)  =  -15a /  (8a)  =   -15/8

So

a/2 =  -15/8

a = -15/4

Here's another way

cos B  =  sqrt (1 - sin^2B)  =  sqrt ( 1 - 25/49 )  =  sqrt ( 49 -25) / 7  =  sqrt ( 24)  / 7  =   

2sqrt (6)  /  7        (as BuilderBoi found !!!)

This is an unusual problem  !!!

See the graph here :

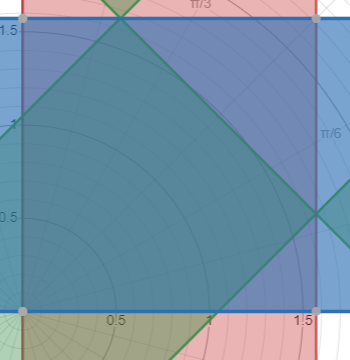
The  feasible area  =  (pi/2)^2  = pi^2/4

When x  = 0

sin (0)   - sin (y) + sin^2 (y)  =  3/4

1  - sin(y) +sin^2(y)  = 3/4

sIn^2 (y) - sin (y)  = -1/4

sin^2(y) - sin (y) + 1/4 = 0

(sin y - 1/2)^2  = 0

sin y  =  1/2

arcsin (1/2)  =  y

When  y =pi/2   we have (similarly)

sin^2 (x) -sin (x) + 1  =  3/4

sin^2 (x) -sin x = -1/4

sin^2 (x) - sin (x) + 1/4)  = 0

(sin x -1/2)^2 = 0

sin x  = 1/2

arcsin (1/2) = x

This sets  up  the area of  the two  right triangles  in the upper left and lower right of the feasible region

The area of these two right triangles  = ( pi/2 - arcsin (1/2)) ( arcsin (1/2))  

And the larger right triangle in the upper right corner has the area  (1/2) (pi/2- arcsin (1/2)^2

So  the area under consideration  =

2.4674  - .5483  - .5483 

pi^2 / 4   -  (pi/2 - arcsin (1/2))(arcsin (1/2))  - (1/2)(pi/2 -arcsin (1/2))^2  =   5pi^2  / 36