CPhill

Add the fractions

1/3 + 3/10 + 1/5  =

10/30 + 9/30 + 6/30  =   25/30 =  5/6  spent on eveything else  but the  burgers

So  1/6  of the circle  is  the fraction of $30 spent on the  burgers =   (1/6 ) (30) =  $5  on burgers

I believe you  left out  something.....

aaa,bbb    isn't a 9 digit number

Area of  X  = 4^2 * pi    =  16 pi

Area of Y  =   (6^2 - 4^2) * pi  =  (36 - 16) * pi   =  20 pi

Area of Z =  (9^2 - 6^2) * pi  =  (81 - 36) * pi =  45 pi

[ Largest Area ] - [ Smallest Area ]  =   45 pi  - 16 pi  =     29 pi

Thx, choutowne.....your answer is correct  ( I made a math error calculating the  distance  of AP)

I have since  corrected my answer !!!

*****

\(\frac{-3\pm i\sqrt{327}}{14}\)

By Vieta, the product of the roots =   k/ 7

So

[ -3 + sqrt (227) i ]  * [ -3 - sqrt (227)i ] / 14^2  =  k /7

[9 - 227 * i^2]  =   14^2 k / 7                   ( i^2 = -1)

[9 + 227] = 14^2 k / 7

236 * 7 / 14^2   =  k

59/7 =  k

Note that an integer that can  be  expressed as 2^n   has the sum of its proper divisors  =  2^n  - 1

Example   8 =  2^3

Proper   divisors =  1,2,4    sum = 7 =   2^3 - 1  

So

256  =  2^8

Sum of  proper divisors =  2^8 - 1 =   255

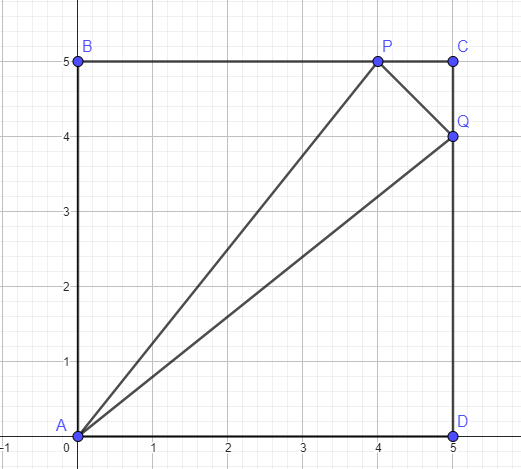
Since PC and QC = 1, then PQ = sqrt (2)

Let A = (0,,0)  and P = (4,5) so AP  =sqrt [ 4^2 + 5^2]  = sqrt (41)  = AQ

So....by Law of Cosines

PQ^2  = AP^2 + AQ^2 -2 (AP)(AQ) cos (PAQ)

2 = 41 + 41  - 2 (sqrt 41)( sqrt 41) cos (PAQ)

-80 / (- 2 * 41 ) =  cos PAQ

80 /82  =  40/41  cos PAQ

sin PAQ =   sqrt  [ 1 - (40/41)^2 ] =   sqrt  [ 41^2 - 40^2] / 41  =  sqrt (81) / 41 =  9 / 41

CORRECTED ANSWER  !!!!