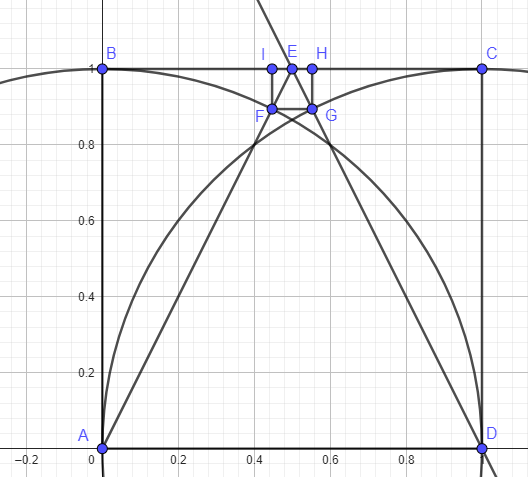
Let A = (0,0) B = (0,1) C = (1,1) and D = (1,0)
Let the equation of the circle on the left be
x^2 + y^2 = 1
We can locate a point at the midpoint of both squares at E = (1/2, 1)
Connect AE.....
And we can call the intersection of AE and the left circle, F
And the distance between F and BC = FI = one side of the square we are looking for
And by similarity BE / EA = !E/ EF
And the equation of the line through AE is y = 2x
Sub this into the equation of the circle for y so we can find the intersection point of the line and the circle
This will be point F
x^2 + (2x)^2 = 1
x^2 + 4x^2 = 1
5x^2 = 1
x^2 = 1/5
x= 1/sqrt 5
y = 2/sqrt 5
So F = (1/sqrt 5, 2/sqrt 5)
The circle on the right has the equation (x -1)^2 + y^2 =1
And by symmetry point G is the intersection of ED and this circle = (1 - x , y) = (1 - 1/sqrt5 , 2/sqrt5 )
The side of the square = FG = FI = (1 - 1/sqrt 5) - 1/sqrt5 = 1 -2/sqrt5
Then its area = (1 - 2/sqrt5)^2 = 1 - 4/sqrt 5 + 4/5 = [ 9 + 4sqrt 5 ] / 5


