Nothing shown, but I assume you want the area of the large square ???
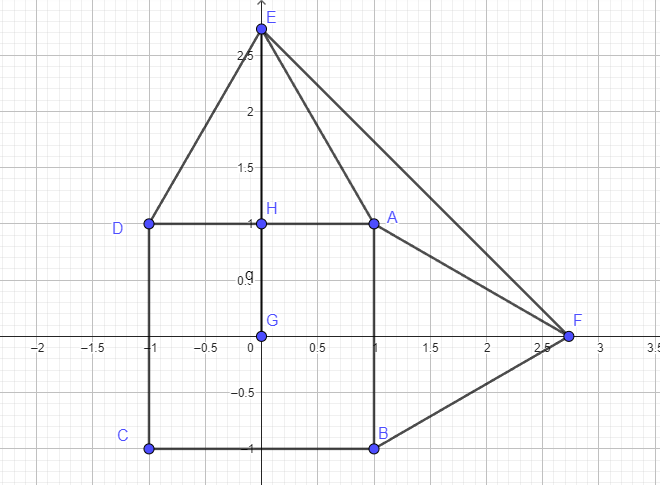
Let G = (0,0)
Let HG = 1
Using the Pythagorean Theorem, the height of one of the equilateral triangles = sqrt (EA^2 - HA^2) = sqrt ( 2^2 -1^2) = sqrt (3)
So E = ( 0, HG + HE) = (0, 1 + sqrt (3))
And by symmetry, F = (1 + sqrt 3, 0)
The distance between these points = EF = the side of the large square = sqrt [ (1 + sqrt 3)^2 + (1 + sqrt 3)^2 ] =
sqrt [ 2 * ( 1 + sqrt 3)^2 ]
So....the area of the larger square = EF^2 = 2 * (1 + sqrt 3)^2 = 2 * (4 +2sqrt 3) =
8 + 4sqrt 3 =
4 ( 2 + sqrt 3)


