CPhill

\((a\circ b)(3) - (b\circ a)(3) \)

b(3)  = 2(3) - 5    = 1

a(3)  = 2(3) + 5 = 11

a[b(3)] - b[a(3) ]  = 

a (1) - b(11)  =

[ 2(1) + 5 ] - [ 2(11) -5 ]  =

        7  -  17  =

          -10

The freshmen  can occupy any 4 positions

And for  each of  these  they can be arranged in 4! = 24 ways

And the sophomores can  occupy any of the  other 3 positions and  can  be arranged in 3! = 6 ways

So

4 * 24 *  6  =  

576 arrangements

Here :

https://web2.0calc.com/questions/functions_78352

The triangle is  equilateral

Let YZ be the base

Let the center of the semi-circle = (5,0)

Let Y = (0,0)

Let the equation of the line through  YX  be

y =sqrt (3) x

sqrt (3)x - y  =  0

Using the formula for the distance  between  a point and a  line, we  can find the radius as

r  = abs [ sqrt 3 *(5)  - 1(0) / sqrt [ (sqrt (3))^2 + (-1)^2 ]  = 5sqrt (3) / 2

Area =  (1/2)pi * ( 25 * 3  / 4)  =  (75 / 8)  pi

f(x)  = f(f(x)) + 16x + 5

x^2  - 3x + 1 =   [ x^2 - 3x + 1]^2 -3[ x^2 - 3x + 1] + 1 + 16x + 5 

x^2 - 3x + 1 =  x^4 - 6 x^3 + 11 x^2 - 6 x + 1 -3x^2 + 9x - 3 + 1 + 16x + 5

x^4 -6x^3 + 7x^2+ 22x -3  =  0

By graph, the solutions  for  x are

x ≈ -1.2305 

x ≈  -0.14377

y=3x + 2    (1)

(x-4)^2 + (y -5)^2  = 68   

The center of the circle is  (4, 5)

The slope  of the given line is  3

The slope of a perpendicular line is  -1/3

Using (4,5)  and writing an equation for this perpendicular  line gives us

y = -(1/3)(x -4) + 5

y = (-1/3)x + 4/3 + 5

y = (-1/3)x + 19/3

Finding the x intersection of these  two lines

3x + 2 = (-1/3)x + 19/3

9x + 6 = -x + 19

10x = 13

x = 13/10 

y = 3(13/10) + 2 =  47/4

The coordinates of the  midpoint  = (13/10, 59/10)

Call the center of one  of the semi-circles  = D

Call the center of the small circle = O

Call the radius of the small circle  = r

Triangle  OBD  is  right such that

BD  =1

OB =  2 - r

OD =  2 + r

BD^2 + OB^2  = OD^2

1^2  + ( 2 - r)^2  = (1 + r)^2

1 + r^2 - 4r + 4  =  r^2 + 2r + 1

6r  = 4

r = 4/6  =  2/3

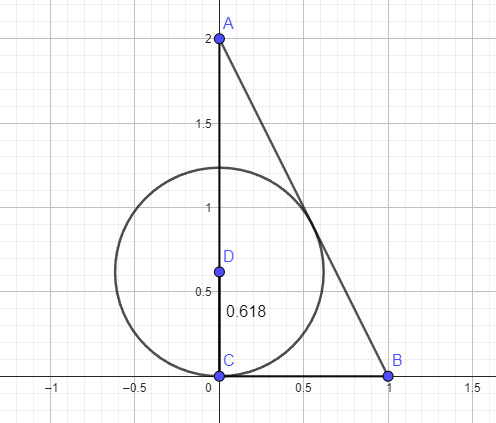
Let C = (0,0)

Let A = ( 0,2)

Let B  = (1,0)

Equation of  line through AB     

y  = (-2)x + 2

2x + y - 2   = 0

We can find the radius  thusly

Call the center of the  semi-circle (0,r)

One point of tangency will be at C

Distance from the center of the  semi-circle to BC =  r    (1)          

Using the equation that gives us the distance from (0,r)  to the line 2x + y - 2 = 0

abs  [ 2(0) + 1(r) - 2 ] / [ 2^2 + 1^2 ]     (2)

Equate  (1) , (2)    and note that  r < 2

r  =  abs  [ 2(0) + r - 2 ]  /  sqrt [ 2^2 + 1^2 ] 

r = abs [ 2 - r ] / sqrt (5)

sqrt (5)r  =  2 - r

sqrt (5)r + r =  2

r [ 1 + sqrt (5)] = 2

r =  2 / [ 1 + sqrt (5) ]   = phi   ≈  .618  = DC

Depends on the location of C

CM  has no definite length

The location of M will remain constant

CM here =  7

If C  moves to D, then CM  =  8

Let the radius of the smallest circle = 1     Area = pi

Then

A2  =  pi (radius of second circle) - area of first circle

pi = pi r^2  - pi

2pi = pi  r^2

2 = r^2

r = sqrt (2)

pi = pi ( [ radius of third circle]^2 - [radius of second circle ] ^2)

1 = [ radius of third circle] ^2    - [sqrt 2]^2

1 = radius of third circle^2   -2

3 = radius of third circle ^2

sqrt (3)  =radius of third circle

pi = pi [ radius of fourth circle  ^2 - radius of  third circle ^2 ] 

1 = radius of fourth circle^2 - (sqrt 3)^2

1 = radius of fourth circle^2 - 3

4 = radius of fourth circle^2

2 = radis of  fourth circle

r4 / r1  =  2  / 1   =  2

  fourth circle = 2