CPhill

https://web2.0calc.com/questions/coordinates_80366

                P

       5                    8

Q               M                   R

        5.5              5.5

Note that cos RMP = -cos QMP

Law of Cosines

PQ^2   = QM^2 + PM^2 - 2 (QM * PM) cos (QMP)    

PR^2  =  RM^2  + PM^2 - 2(RM * PM)(-cos (QMP)   

5^2 = 5.5^2 + PM^2 - 2(5.5 * PM) cos (QMP)

8^2 = 5.5^2 + PM^2 + 2(5.5 *PM) cos (QMP)      add these

89 = 60.5 + 2PM^2

28.5 = 2PM^2

PM =  sqrt [ 28.5 / 2 ]  ≈  3.77 

x ( x + 6) >  16 - 5x + 33        simplify as

x^2 + 11x - 33   >  0          set up  as an equality....use the quad formula to find the roots

x =  [ -11 + / - sqrt [ 11^2 - 4 * 1 * -33 ] ] / 2

x = [ -11 +/ -  sqrt 253 ] /2

This is a parabola intersecting the x axis......we are interested in the parts lying above the axis

These are  ( -inf, (-11 - sqrt 253 ) / 2 ) U ( (-11 +  sqrt 253) / 2 , inf) =  solution

Sum =  (140) (141) / 2 =  = 70 * 141  

70  = 2 * 7  * 5

141 = 3 * 47

So

   70         *       141  = 

(2 * 7 * 5)  *   ( 3 * 47 )

47 is the greatest prime divisor

4t^2 ≤ -9t + 12 -14t + 36             simplify as

4t^2 + 23t -48  ≤ 0            set as an inequaity

4t^2 + 23t - 48 = 0       use the quadratic formula   to find the roots

[ -23 +/- sqrt [ 23^2 - 4*4*-48 ] /  (2*4)     =  t

[-23 +/-  sqrt [ 1297 ] / 8  = t

This is a parabola which intersects the x axis....the part lying between the roots will be the answer

So....the solution is

[ -23 - sqrt 1297 ] /8   ≤  t   ≤  [ -23 + sqrt 1297] / 8

Simplify as

2x - 4y + 3z = 10

4x - 9y - 14z = 7

kx -5y + z  = 3

This will have no solutions when the discriminant = 0 .....so....

2   -4     3     2     -4

4  -9    -14    4    -9 =    D  =  0

k   -5     1     k     -5

[ 2*-9*1  + -4*-14*k + 3 * 4 * -5 ]  - [ k* -9* 3 + -5 * -14 * 2 + 1*4*-4 ] =  0

[ -18 + 56k - 60] - [ -27k + 140 - 16 ]  =0 

[ -78 +56k ] - [ 124 - 27k ]  = 0

-202 + 83k  = 0

83k = 202

k = 202 / 83

If possible, triangle APS  would be a right triangle with legs PS  and AS  and hypotenuse AP

But  the hypotenuse is always longer than either leg so this  triangle is impossible.

We have that

PX * QX = RX * SX

Let RX = s   and  SX = (38 -s)

So

38 * 36  =  s * (38 -s)

1368 = 38s - s^2                rearrange as

s^2 - 38s  + 1368  = 0

(This has no  real  solution for s  !!! )

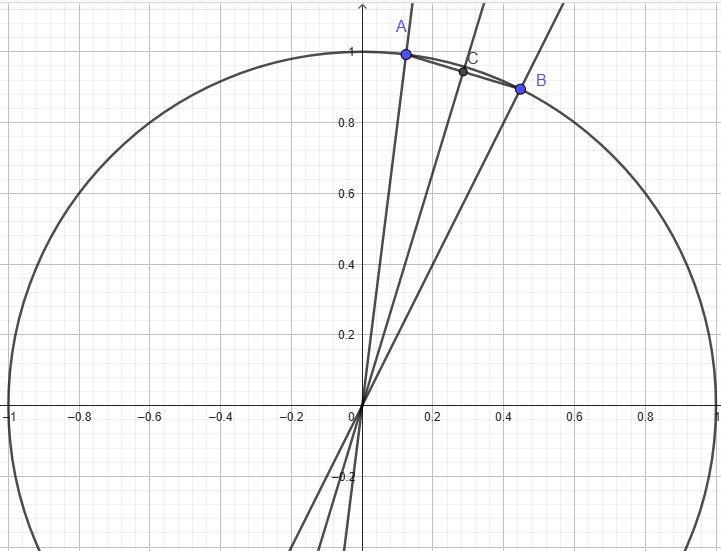
Construct a circle centered at the origin with a radius of 1

Let the line with the slope of 8 be y =8x =  (8/1)x

Let the line with the slope of 2 be y = 2x = (2/1)x

Let the point where the line with the slope of 8x intersects the circle be

(1/sqrt (1^2 + 8^2) / 8/(sqrt (1^2 + 8^2)) =

( 1/sqrt65 , 8/sqrt 65 )  = A

Let the point where the line with the slope of 2x intersects the circle be 

(1/sqrt (1^2 + 5^2) , 2/sqrt (1^2 + 2^2)) =

(1/sqrt 5 , 2/sqrt 5) = B

Draw AB

The midpoint of this segment is

[ (1/sqrt 65 + 1/sqrt 5) /2  , (8/sqrt 65 + 2/sqrt 5) /2 ] = 

[ ( sqrt 5 + sqrt 65) /2 ,(8sqrt 5 + 2 sqrt 65) /2 ]  =

[ (sqrt 5/ 2) ( 1 + sqrt 13) , (sqrt 5/ 2) ( 8 + 2sqrt 13) ] =  C

The slope of the line through the origin through C is

[ 8 + 2sqrt 13 ] / [ (1 +  sqrt 13 ]  =

[ 8 + 2sqrt 13 ] [1 - sqrt 13 ] [ 1 -13] =

[ 8 + 2sqrt 13 - 8sqrt 13 - 26 ] /[ -12] = 

[ -18 - 6sqrt13 ] / [-12]  =

[ 3 + sqrt 13 ] / 2  =slope of line bisecting the acute angle between these lines

The exterior angle would measure

[ 8 ] / [ 4 + 2 + 8 ]  * 360  = 

[ 8 ] / [ 14 ] * 360  =

[ 4/ 7] * 360 ≈  205.7°   

Which is impossible because the sum of the exterior angle and its  corresponding interior angle can  never  measure more than 180°