heureka

Thank you, CoolStuffYT!

Thank you, CPhill !

Thank you, Melody !

question:

\(\lambda=\mu \\ \dfrac{1}{2}\lambda=1-\mu \\ 1-\lambda=\dfrac{1}{2}\mu \\ \lambda=\mu=?\)

\(\begin{array}{|lrcll|} \hline (1) & \dfrac{1}{2}\lambda &=& 1-\mu \\ & \dfrac{1}{2}\lambda+\mu &=& 1 \quad | \quad \times 4 \\ & \mathbf{2\lambda+4\mu} &=& \mathbf{4} \\\\ (2) & 1-\lambda &=& \dfrac{1}{2}\mu \\ & \lambda +\dfrac{1}{2}\mu &=& 1 \quad | \quad \times 2 \\ & \mathbf{2\lambda + \mu} &=& \mathbf{2} \\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline (1) & \mathbf{2\lambda+4\mu} &=& \mathbf{4} \\ (2) & \mathbf{2\lambda + \mu} &=& \mathbf{2} \\ \hline (1)-(2): & 4\mu- \mu &=& 4-2 \\ & 3\mu &=& 2 \\ & \mathbf{ \mu } &=& \mathbf{\dfrac{2}{3}} \\ \hline \end{array} \)

\(\lambda=\mu=\mathbf{\dfrac{2}{3}}\)

 Let \(a\), \(b\), \(c\) be the roots of \(x^3 - 17x - 19\).  Find \(a^3 + b^3 + c^3\).

\(\begin{array}{|rcll|} \hline && x^3 - 17x - 19 \\ &=& x^3 + {\color{red}0}x^2 {\color{green}-17}x {\color{blue}-19} \\\\ \hline \mathbf{\text{vieta:}}\\ {\color{red}0} &=& -(a+b+c) \\ \mathbf{a+b+c} &=& \mathbf{0} \\\\ {\color{green}-17} &=& ab+ac+bc \\ \mathbf{ab+ac+bc} &=& \mathbf{-17} \\\\ {\color{blue}-19} &=& -abc \\ \mathbf{abc} &=& \mathbf{19} \\ \hline \end{array} \)

 Formula:

\(\begin{array}{|rcll|} \hline a^3+b^3+c^3 &=& 3\underbrace{abc}_{=19}+\underbrace{(a+b+c)}_{=0}\left(a^2+b^2+c^2-(ab+bc+ca)\right) \\ a^3+b^3+c^3 &=& 3\times 19 \\ \mathbf{a^3+b^3+c^3} &=& \mathbf{57} \\ \hline \end{array}\)

Each side of a regular dodecagon A1 A2 A3 ... A12 has length 2. What is the area of the pentagon A1 A2 A3 A4 A5?

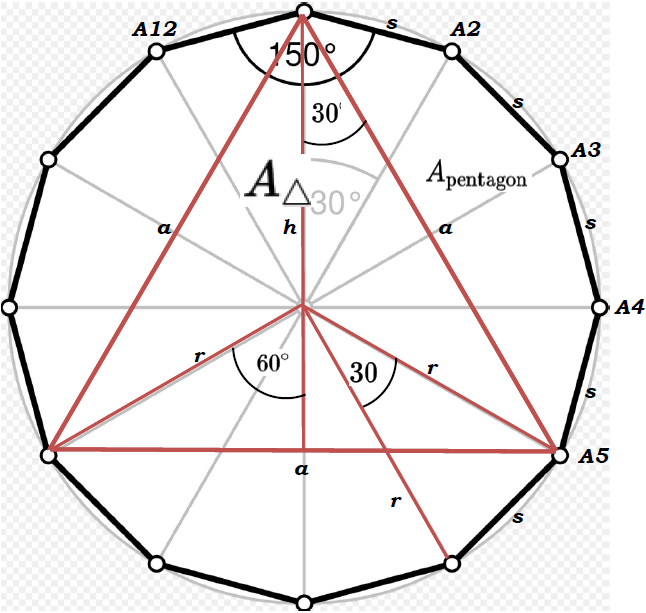
\(\text{Let side of a regular dodecagon $=s $} \\ \text{Let radius of the circle $=r $} \\ \text{Let area of the dodecagon $=A_{\text{dodecagon}} $} \\ \text{Let area of the pentagon $=A_{\text{pentagon}} $} \\ \text{Let area of the triangle in the center $=A_{\triangle} $} \)

\(\begin{array}{|rcll|} \hline A_{\text{dodecagon}} &=& 3\times A_{\text{pentagon}} + A_{\triangle} \\ \mathbf{A_{\text{pentagon}}} &=& \mathbf{\dfrac{1}{3} \left( A_{\text{dodecagon}} - A_{\triangle}\right)} \quad | \quad \boxed{A_{\text{dodecagon}}= 3(2+\sqrt{3})s^2} \\ \hline \end{array} \)

\(\mathbf{r=\ ?}\)

\(\begin{array}{|rcll|} \hline \sin(15^\circ) &=& \dfrac{\dfrac{s}{2}}{r} \\ 2r &=& \dfrac{s}{\sin(15^\circ)} \quad | \quad \sin(15^\circ) = \dfrac{1}{4}\sqrt{2}(\sqrt{3}-1) \\ \mathbf{2r} &=& \mathbf{\dfrac{4s}{\sqrt{2}(\sqrt{3}-1)}} \\ \hline \end{array} \)

\(\mathbf{a=\ ?}\)

\(\begin{array}{|rcll|} \hline \sin(60^\circ) &=& \dfrac{\dfrac{a}{2}}{r} \\ a &=& 2r\sin(60^\circ) \quad | \quad \sin(60^\circ) = \dfrac{\sqrt{3}}{2} \\ a &=& 2r\dfrac{\sqrt{3}}{2} \\ \mathbf{a} &=& \mathbf{\dfrac{4s}{\sqrt{2}(\sqrt{3}-1)}\dfrac{\sqrt{3}}{2}} \\ \hline \end{array}\)

\(\mathbf{h=\ ?}\)

\(\begin{array}{|rcll|} \hline \cos(30^\circ) &=& \dfrac{h}{a} \\ h &=& a\cos(30^\circ) \quad | \quad \cos(30^\circ) = \dfrac{\sqrt{3}}{2} \\ h &=& a\dfrac{\sqrt{3}}{2} \\ h &=& \dfrac{4s}{\sqrt{2}(\sqrt{3}-1)}\dfrac{\sqrt{3}}{2}\dfrac{\sqrt{3}}{2} \\ h &=& \dfrac{4s}{\sqrt{2}(\sqrt{3}-1)}\dfrac{3}{4} \\ \mathbf{h} &=& \mathbf{\dfrac{3s}{\sqrt{2}(\sqrt{3}-1)}} \\ \hline \end{array}\)

\(\mathbf{A_{\triangle}=\ ?}\)

\(\begin{array}{|rcll|} \hline A_{\triangle} &=& \dfrac{ah}{2} \\ &=& \dfrac{1}{2}\dfrac{4s}{\sqrt{2}(\sqrt{3}-1)}\dfrac{\sqrt{3}}{2}\dfrac{3s}{\sqrt{2}(\sqrt{3}-1)} \\ &=& \dfrac{3\sqrt{3}}{2\left(\sqrt{3}-1 \right)^2}s^2 \quad | \quad \left(\sqrt{3}-1 \right)^2 =2(2-\sqrt{3}) \\ &=& \dfrac{3\sqrt{3}}{2*2(2-\sqrt{3})}s^2 \\ \mathbf{A_{\triangle}} &=& \mathbf{ \dfrac{3\sqrt{3}}{4(2-\sqrt{3})}s^2 } \\ \hline \end{array} \)

\(\mathbf{A_{\text{pentagon}}=\ ?}\)

\(\begin{array}{|rcll|} \hline \mathbf{A_{\text{pentagon}}} &=& \mathbf{\dfrac{1}{3} \left( A_{\text{dodecagon}} - A_{\triangle}\right)} \quad | \quad \boxed{A_{\text{dodecagon}}= 3(2+\sqrt{3})s^2} \\\\ &=& \dfrac{1}{3} \left( 3(2+\sqrt{3})s^2 - \dfrac{3\sqrt{3}}{4(2-\sqrt{3})}s^2\right) \\ \\ &=& \dfrac{3}{3} \left((2+\sqrt{3}) - \dfrac{\sqrt{3}}{4(2-\sqrt{3})} \right)s^2 \\ \\ &=& \left(\dfrac{4(2-\sqrt{3})(2+\sqrt{3})-\sqrt{3}}{4(2-\sqrt{3})} \right)s^2 \\ \\ &=& \left(\dfrac{4(4-3)-\sqrt{3}}{4(2-\sqrt{3})} \right)s^2 \\ \\ &=& \left(\dfrac{4 -\sqrt{3}}{4(2-\sqrt{3})} \right)s^2 \\ \\ &=& \left(\dfrac{4 -\sqrt{3}}{4(2-\sqrt{3})}\right)\left(\dfrac{2+\sqrt{3}}{2+\sqrt{3}} \right)s^2 \\ \\ &=& \dfrac{ (4 -\sqrt{3}) (2+\sqrt{3}) }{4(2-\sqrt{3})(2+\sqrt{3})} s^2 \\ \\ &=& \dfrac{ (5+2\sqrt{3}) }{4(4-3)} s^2 \\ \\ \mathbf{A_{\text{pentagon}}}&=& \mathbf{ \dfrac{ (5+2\sqrt{3}) }{4 } s^2 } \quad | \quad s = 2 \\ \mathbf{A_{\text{pentagon}}}&=& \mathbf{ 5+2\sqrt{3} } \\ \hline \end{array}\)

A line \(y=mx+b\)  intersects the parabola \(y=x^2\) at points \(A\) and \(B\).
The line \(AB\) intersects the y-axis at the point  \(P\).

If \(AP-BP=1\)  then find \(m^2\).

\(\text{Let $A=(x_A,y_A)=(x_A,x_{A}^2) $} \\ \text{Let $B=(x_B,y_B)=(x_B,x_{B}^2) $} \\ \text{Let $P=(x_P,y_P)=(0,y_P) $} \)

\(\begin{array}{|l&rcll|} \hline BP: & m &=& \dfrac{y_P-y_B}{x_P-x_B} \\ & &=& \dfrac{y_P-x_{B}^2}{0-x_B} \\ &\mathbf{ m}&=& \mathbf{\dfrac{x_{B}^2-y_P}{x_B}} \\\\ AP: & m &=& \dfrac{y_A-y_P}{x_A-x_P} \\ & &=& \dfrac{x_{A}^2-y_P}{x_A-0} \\ &\mathbf{m} &=& \mathbf{\dfrac{x_{A}^2-y_P}{x_A}} \\ \hline \mathbf{ m} & = \mathbf{\dfrac{x_{B}^2-y_P}{x_B}}&=& \mathbf{\dfrac{x_{A}^2-y_P}{x_A}} \\ & x_A(x_{B}^2-y_P) &=& x_B(x_{A}^2-y_P)\\ & x_A x_{B}^2-x_Ay_P &=& x_B x_{A}^2-x_By_P \\ & y_P(x_B-x_A) &=& x_B x_{A}^2-x_A x_{B}^2 \\ & y_P(x_B-x_A) &=& -x_Ax_B(x_B-x_A) \\ (1) & \mathbf{y_P} &=& \mathbf{-x_Ax_B} \\ \hline &\mathbf{ m}&=& \mathbf{\dfrac{x_{B}^2-y_P}{x_B}} \quad | \quad \mathbf{y_P=-x_Ax_B} \\ & m &=& \dfrac{x_{B}^2-(-x_Ax_B)}{x_B} \\ & m &=& \dfrac{x_{B}^2+x_Ax_B}{x_B} \\ & m &=& \dfrac{x_{B}^2}{x_B}+\dfrac{x_Ax_B}{x_B} \\ (2) & \mathbf{m} &=& \mathbf{x_A+x_B} \\ \hline \end{array}\)

\(\begin{array}{|rclrcl|} \hline \mathbf{AP-BP} &=& {1} \qquad \text{or} \qquad BP = AP-1 \\\\ \mathbf{AB} &=& \mathbf{AP+BP} \\ AB &=& AP+AP-1 \\ \mathbf{AB} &=& \mathbf{2AP-1} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline AB^2 &=& (x_A -x_B )^2+(y_A -y_B )^2 \\ &=& (x_A -x_B )^2+\left(x_{A}^2 -x_{B}^2 \right)^2 \\ &=& (x_A -x_B )^2+\Big( (x_{A} -x_{B}) (x_{A} +x_{B}) \Big)^2 \\ &=& (x_A -x_B )^2+ (x_{A} -x_{B})^2 (x_{A} +x_{B})^2 \\ &=& (x_A -x_B )^2 \Big(1 +( \underbrace{x_{A} +x_{B}}_{=m})^2\Big) \\ &=& (x_A -x_B )^2 (1 +m^2 ) \\ \mathbf{AB} &=& \mathbf{(x_A -x_B )\sqrt{1 +m^2} } \\\\ AP^2 &=& (x_A -x_P )^2+(y_A -y_P )^2 \\ &=& (x_A -0 )^2+(x_{A}^2 -y_P )^2 \\ &=& x_{A}^2+(x_{A}^2 -y_P )^2 \quad | \quad y_P=-x_Ax_B \\ &=& x_{A}^2+(x_{A}^2 + x_Ax_B )^2 \\ &=& x_{A}^2+\Big(x_A(\underbrace{x_A+x_B}_{=m}) \Big)^2 \\ &=& x_{A}^2+(x_A\times m)^2 \\ &=& x_{A}^2+x_{A}^2m^2 \\ &=& x_{A}^2(1+m^2) \\ \mathbf{AP} &=& \mathbf{x_A\sqrt{1 +m^2} } \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{AB} &=& \mathbf{2AP-1} \\\\ \mathbf{(x_A -x_B )\sqrt{1 +m^2} } &=& 2\times \mathbf{x_A\sqrt{1 +m^2} } -1 \\ \sqrt{1 +m^2}(x_A-x_B-2x_A) &=& -1 \\ \sqrt{1 +m^2}(2x_A-x_A+x_B) &=& 1 \\ \sqrt{1 +m^2}(\underbrace{x_A+x_B}_{=m}) &=& 1 \\ \sqrt{1 +m^2}\times m &=& 1 \quad \text{square both sides} \\ (1 +m^2)\times m^2 &=& 1 \\ (m^2)^2 + m^2 - 1 &=& 0 \\ m^2 &=& \dfrac{-1\pm \sqrt{1-4*(-1)} }{2} \\\\ m^2 &=& \dfrac{-1 {\color{red}+} \sqrt{1-4*(-1)} }{2} \quad | \quad m^2 > 0 ! \\ \mathbf{m^2} &=& \mathbf{\dfrac{-1 +\sqrt{5} }{2}} \\ \hline \end{array}\)

Thank you, OldTimer !

Thank you, Melody !

Could anyone check if these are correct?

2. is correct !

1.

\(\begin{array}{|rcll|} \hline 0.1x + 0.01 (x - 10) &=& 110.9-x \quad | \quad \times 10 \\ 1x + 0.1 (x - 10) &=& 1109-10x \\ x + 0.1x - 1 &=& 1109-10x \\ 10x +x + 0.1x - 1 &=& 1109 \\ 10x +x + 0.1x &=& 1110 \\ 11.1x &=& 1110 \\ \\ x &=& \dfrac{1110}{11.1} \\ \\ \mathbf{x} &=& \mathbf{100} \\ \hline \end{array}\)

How many distinct triangles with positive integer sides have perimeter equal to 12? 

I assume, the answer is 3 (2,5,5) (3,4,5) (4,4,4)

Moin, ich muss \(3^{47} \pmod {91}\) mit der Methode Multiplizieren & Quadrieren rechnen aber irgendwie check is das gar nicht.

Methode Multiplizieren & Quadrieren:

\(\begin{array}{|rcll|} \hline && \mathbf{ 3^{47} \pmod {91}} \quad &| \quad 3^{47} = 3\cdot \left( 3^{23}\right)^2 \\\\ & \equiv & 3\cdot \left( 3^{23}\right)^2 \pmod {91} \quad &| \quad 3^{23} = 3\cdot \left(3^{11}\right)^2 \\ & \equiv & 3\cdot \left( 3\cdot \left(3^{11}\right)^2\right)^2 \pmod {91} \quad &| \quad 3^{11} = 177147 \\ & \equiv & 3\cdot \left( 3\cdot \left(177147\right)^2\right)^2 \pmod {91} \quad &| \quad 177147 \pmod {91} \equiv 61 \\ & \equiv & 3\cdot \left( 3\cdot \left(61\right)^2\right)^2 \pmod {91} \quad &| \quad 3\cdot \left(61\right)^2 = 11163 \\ & \equiv & 3\cdot \left( 11163 \right)^2 \pmod {91} \quad &| \quad 11163 \pmod {91} \equiv 61 \\ & \equiv & 3\cdot \left( 61 \right)^2 \pmod {91} \quad &| \quad 3\cdot \left(61\right)^2 = 11163 \\ & \equiv & 11163 \pmod {91} \quad &| \quad 11163 \pmod {91} \equiv 61 \\ & \equiv & \mathbf{ 61 \pmod {91} } \\ \hline \end{array}\)