heureka

Thank you, CPhill !

I need help with this system:
\(x(y + z) = 39\\ y(x + z) = 60\\ z(x + y) = 63\)

What is x?

\(\begin{array}{|lrcll|} \hline (1) & x(y + z) &=& 39 \\ (2) & y(x + z) &=& 60 ~\text{or}~ \mathbf{yx+yz = 60} \\ (3) & z(x + y) &=& 63 ~\text{or}~ \mathbf{zx+yz = 63} \\ \hline (1)+(2)+(3): &x(y + z)+ y(x + z)+z(x + y) &=& 39+60+63 \\ & x(y + z) +yx +yz +zx+zy &=& 162 \\ & x(y + z) +x(y+z) +2yz &=& 162 \\ & 2x(y + z) +2yz &=& 162 \quad | \quad :2 \\ & x(y + z) +yz &=& 81 \quad | \quad x(y + z) = 39 \\ & 39 +yz &=& 81 \\ & yz &=& 81-39 \\ & \mathbf{yz} &=& \mathbf{42} \\ \hline & \mathbf{yx+yz} &=& \mathbf{60} \quad | \quad \mathbf{yz = 42} \\ & yx+42 &=& 60 \\ & yx &=& 60-42 \\ & \mathbf{yx} &=& \mathbf{18}~\text{or}~ \mathbf{y=\dfrac{18}{x}} \\ \hline & \mathbf{zx+yz} &=& \mathbf{63} \quad | \quad \mathbf{yz = 42} \\ & zx+42 &=& 63 \\ & zx &=& 63-42 \\ & \mathbf{zx} &=& \mathbf{21}~\text{or}~ \mathbf{z=\dfrac{21}{x}} \\ \hline & \mathbf{yz} &=& \mathbf{42} \\ & \dfrac{18}{x}*\dfrac{21}{x}&=& \mathbf{42} \\ & 42x^2 &=& 18*21 \\ & x^2 &=&\dfrac{18*21}{42} \\ & x^2 &=& \dfrac{3*6*3*7}{6*7} \\ & x^2 &=& 3*3 \\ & \mathbf{x} &=& \mathbf{3} \\ \hline & \mathbf{y} &=& \mathbf{\dfrac{18}{x}} \\ & y &=& \dfrac{18}{3} \\ & \mathbf{y} &=& \mathbf{6} \\ \hline & \mathbf{z} &=& \mathbf{\dfrac{21}{x}} \\ & z &=& \dfrac{21}{3} \\ & \mathbf{z} &=& \mathbf{7} \\ \hline \end{array}\)

Two 2*8 rectangles overlap, as shown below.
Find the area of the overlapping region (which is shaded)

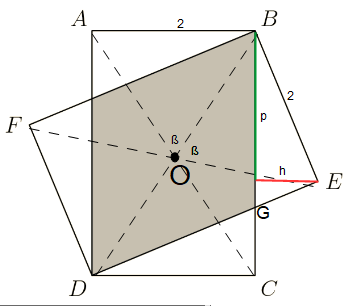
\(\text{Let $O=(0,0)$} \\ \text{Let $A=(-1,4)$} \\ \text{Let $B=(1,4)$} \\ \\ \text{Let $E=(x_E,y_E)$} \\ \text{Let area of rectangle $=2*8$ } \\ \text{Let area of triangle $[BEG]=\dfrac{\overline{BG}*h}{2}$ } \\ \text{Let the gray area $=$ area of rectangle$-2*$ area of triangle $[BEG]$ } \\ \text{Let the gray area $= \mathbf{2*8-\overline{BG}*h}$ } \\ \text{Let $h=x_E-x_B$} \\ \text{Let $p=y_B-y_E$} \\ \text{Let $\overline{AB}=\overline{BE}=2$} \\ \text{Let $\overline{BE}^2=p*\overline{BG}$} \)

1. rotate

\(\begin{array}{|lrcll|} \hline \text{Rotation matrix } \\ & R&=&\begin{bmatrix} \cos(ß)&\sin(ß) \\ - \sin(ß)&\cos(ß) \\ \end{bmatrix} \\ & B&=&R\cdot A \\\\ & \begin{bmatrix} x_B\\y_B\end{bmatrix} &=&\begin{bmatrix} \cos(ß)&\sin(ß) \\ - \sin(ß)&\cos(ß) \\ \end{bmatrix} \begin{bmatrix} x_A\\y_A\end{bmatrix} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \begin{bmatrix} 1\\4\end{bmatrix} &=&\begin{bmatrix} \cos(ß)&\sin(ß) \\ - \sin(ß)&\cos(ß) \\ \end{bmatrix} \begin{bmatrix} -1\\4\end{bmatrix} \\\\ -\cos{ß}+4\sin(ß) &=& 1 \qquad (1) \\ \sin{ß}+4\cos(ß) &=& 4 \qquad (2) \\ \\ \mathbf{\sin(ß)} &=& \mathbf{\dfrac{8}{17}} \\\\ \mathbf{\cos(ß)} &=& \mathbf{\dfrac{15}{17}} \\ \hline \end{array}\)

2. rotate

\(\begin{array}{|rcll|} \hline \begin{bmatrix} x_E\\y_E\end{bmatrix} &=&\begin{bmatrix} \cos(ß)&\sin(ß) \\ - \sin(ß)&\cos(ß) \\ \end{bmatrix} \begin{bmatrix} 1\\4\end{bmatrix} \\\\ \cos{ß}+4\sin(ß) &=& x_E \qquad (3) \\ x_E &=& \dfrac{15}{17} + 4*\dfrac{8}{17} \\ \mathbf{x_E} &=& \mathbf{\dfrac{47}{17}} \\\\ -\sin{ß}+4\cos(ß) &=& y_E \qquad (4) \\ y_E &=& \dfrac{8}{17} + 4*\dfrac{15}{17} \\ \mathbf{y_E} &=& \mathbf{\dfrac{52}{17}} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{h}&=&\mathbf{x_E-x_B} \\\\ h&=&\dfrac{47}{17}-1 \\\\ \mathbf{h}&=&\mathbf{\dfrac{30}{17}} \\\\ \hline \mathbf{p} &=& \mathbf{y_B-y_E} \\\\ p &=& 4- \dfrac{52}{17} \\\\ \mathbf{p}&=&\mathbf{\dfrac{16}{17}} \\\\ \hline \mathbf{\overline{BE}^2} &=& \mathbf{p*\overline{BG}} \quad | \quad BE=2 \\ 2^2 &=& \dfrac{16}{17}*\overline{BG} \\ \overline{BG} &=& \dfrac{4}{\dfrac{16}{17}} \\\\ \mathbf{\overline{BG}} &=& \mathbf{\dfrac{17}{4}} \\\\ \hline \mathbf{\text{Gray area }} &=& \mathbf{2*8-\overline{BG}*h} \\ &=& \mathbf{2*8-\dfrac{17}{4}*\dfrac{30}{17}} \\\\ &=& 2*8-\dfrac{30}{4} \\\\ &=& 16-\dfrac{15}{2} \\\\ &=& \dfrac{32-15}{2} \\\\ &=& \dfrac{17}{2} \\\\ \mathbf{\text{Gray area }} &=& \mathbf{8.5} \\ \hline \end{array}\)

If \(\omega^3 = 1\) and \(\omega \neq 1\),

then compute \((1 - \omega + \omega^2)(1 + \omega - \omega^2)\).

My attempt:

\(\begin{array}{|rcll|} \hline \mathbf{ (1 - \omega + \omega^2)(1 + \omega - \omega^2) } \\ &=& \Big(1 - (\omega - \omega^2)\Big) \Big(1 + (\omega - \omega^2)\Big) \\ &=& 1 - (\omega - \omega^2)^2 \\ &=& 1 - (\omega^2 - 2\omega^3+\omega^4) \quad | \quad \omega^3=1 \\ &=& 1 - (\omega^2 - 2+\omega^4) \quad | \quad \omega^4=\omega^3*\omega=\omega \\ &=& 1 - (\omega^2 - 2+\omega) \\ &=& 3 - (\omega^2 + \omega) \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline (\omega^2 + \omega)^2 &=& \omega^4 + 2\omega^3 + \omega^2 \quad | \quad \omega^3=1 \\ (\omega^2 + \omega)^2 &=& \omega^4 + 2 + \omega^2 \quad | \quad \omega^4=\omega^3*\omega=\omega \\ (\omega^2 + \omega)^2 &=& \omega + 2 + \omega^2 \\ (\omega^2 + \omega)^2 &=& \omega^2 + \omega + 2 \\ (\omega^2 + \omega)^2- (\omega^2 + \omega) - 2 &=& 0 \quad | \quad \omega^2 + \omega = x \\ \mathbf{x^2-x-2} &=& \mathbf{0} \\\\ x &=& \dfrac{1\pm\sqrt{1-4*(-2)}}{2} \\ x &=& \dfrac{1\pm\sqrt{9}}{2} \\ x &=& \dfrac{1\pm3}{2} \\\\ x_1 &=& \dfrac{1+3}{2} \\ x_1&=& 2 \\ \omega^2 + \omega &=& 2 \qquad \text{no solution!} \\ && \boxed{\omega \ne 1 } \\\\ x_2 &=& \dfrac{1-3}{2} \\ x_2 &=& -1 \\ \mathbf{\omega^2 + \omega }&=& \mathbf{-1} \\ \mathbf{ (1 - \omega + \omega^2)(1 + \omega - \omega^2) } &=& 3 - (\omega^2 + \omega) \\ &=& 3 - (-1) \\ \mathbf{ (1 - \omega + \omega^2)(1 + \omega - \omega^2) }&=& \mathbf{ 4 } \\ \hline \end{array}\)

The fifth term of an arithmetic sequence is 9 and the 32nd term is 84.

What is the 23rd term?

\(\begin{array}{|lrcll|} \hline (1) & a_i &=& a_1+(i-1)d \\ (2) & a_j &=& a_1+(j-1)d \\ (3) & a_k &=& a_1+(k-1)d \\ \hline & a_1 = a_i-(i-1)d &=& a_j-(j-1)d \\ & a_i-(i-1)d &=& a_j-(j-1)d \\ & a_j-a_i &=& (j-1)d-(i-1)d \\ & a_j-a_i &=& \Big((j-1)-(i-1)\Big)d \\ (4) & \mathbf{a_j-a_i} &=& \mathbf{(j-i)d} \\ \hline & a_1 = a_j-(j-1)d &=& a_k-(k-1)d \\ & a_j-(j-1)d &=& a_k-(k-1)d \\ & a_k-a_j &=& (k-1)d-(j-1)d \\ & a_k-a_j &=& \Big((k-1)-(j-1)\Big)d \\ (5)& \mathbf{a_k-a_j} &=& \mathbf{(k-j)d} \\ \hline \dfrac{(4)}{(5)}: & \dfrac{a_j-a_i}{a_k-a_j}&=& \dfrac{(j-i)d}{(k-j)d} \\\\ & \dfrac{a_j-a_i}{a_k-a_j}&=& \dfrac{(j-i)}{(k-j)} \\\\ & \ldots \\ & \mathbf{a_k} &=& \mathbf{a_j*\dfrac{(k-i)}{(j-i)}+a_i*\dfrac{(k-j)}{(i-j)}} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline i=5 \qquad a_i &=& 9 \\ j=32 \qquad a_j &=& 84 \\ k=23 \qquad a_k &=& \ ? \\ \hline \mathbf{a_k} &=& \mathbf{a_j*\dfrac{(k-i)}{(j-i)}+a_i*\dfrac{(k-j)}{(i-j)}} \\ a_{23} &=& 84*\dfrac{(23-5)}{(32-5)}+9*\dfrac{(23-32)}{(5-32)} \\ a_{23} &=& 84*\dfrac{18}{27}+9*\dfrac{-9}{-27} \\ a_{23} &=& \dfrac{84*18+9*9}{27} \\ a_{23} &=& \dfrac{84*2+9}{3} \\ a_{23} &=& \dfrac{177}{3} \\ \mathbf{a_{23}} &=& \mathbf{59} \\ \hline \end{array}\)

In triangle \(ABC\), \(\angle ABC = 2 \alpha\) and \(\angle ACB = 140 ^\circ - \alpha\).
\(D\) is a point on line segment \(AB\) such that \(CB = BD\).
What is the measure (in degrees) of \(\angle DCA\)?

\(\text{Let $\angle DCA=x$} \\ \text{Let $\angle BDC=\angle BCD= \beta$} \)

\(\begin{array}{|rcll|} \hline \mathbf{2\alpha + 2\beta} &=& \mathbf{180^\circ} \\ \alpha + \beta &=& 90^\circ \\ \mathbf{\beta} &=& \mathbf{90^\circ -\alpha} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{140^\circ-\alpha} &=& \mathbf{x + \beta} \quad | \quad \mathbf{\beta=90^\circ -\alpha} \\ 140^\circ-\alpha &=& x + 90^\circ -\alpha \\ 140^\circ&=& x + 90^\circ \\ x &=& 140^\circ-90^\circ \\ \mathbf{x} &=& \mathbf{50^\circ} \\ \hline \end{array}\)

D,E,F are the feet of the altitudes in triangle ABC.
Find angle DEF (in degrees).

\(\text{Let $\angle[DEF]=x$} \\ \text{Let $AB=a$, $AC=b$, $BC=c$} \\ \text{Let $\angle[CBE]=90^\circ-65^\circ=25^\circ$} \\ \text{Let $\angle[EBF]=90^\circ-75^\circ=15^\circ$} \\ \text{Let $BF=c*\cos(40^\circ)$, $BD=a*\cos(40^\circ)$} \\ \text{Let $BE=\dfrac{a*c}{b}\sin(40^\circ)$ } \\ \text{Let $\angle[BDE]=D$, $\angle[BFE]=E$} \\ \text{Let $x =360^\circ-(D+E+40^\circ)=320^\circ-(D+E)$}\)

\(\begin{array}{|rcll|} \hline \tan(D) &=& \dfrac{BE*\sin(25^\circ)}{BD-BE*\cos(25^\circ)} \\\\ \tan(D) &=& \dfrac{\dfrac{a*c}{b}*\sin(40^\circ)*\sin(25^\circ)}{a*\cos(40^\circ)-\dfrac{a*c}{b}\sin(40^\circ)*\cos(25^\circ)} \times \dfrac{a}{a} \\\\ \tan(D) &=& \dfrac{\dfrac{c}{b}*\sin(40^\circ)*\sin(25^\circ)}{\cos(40^\circ)-\dfrac{c}{b}\sin(40^\circ)*\cos(25^\circ)} \\\\ && \boxed{ \dfrac{c}{b} = \dfrac{\sin(75^\circ)} {\sin(40^\circ)} } \\\\ \tan(D) &=& \dfrac{\sin(75^\circ)*\sin(25^\circ)}{\cos(40^\circ)-\sin(75^\circ)*\cos(25^\circ)} \\\\ D &=& -75^\circ~ \text{or}~ \mathbf{D=105^\circ} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \tan(E) &=& \dfrac{BE*\sin(15^\circ)}{BF-BE*\cos(15^\circ)} \\\\ \tan(E) &=& \dfrac{\dfrac{a*c}{b}*\sin(40^\circ)*\sin(15^\circ)}{c*\cos(40^\circ)-\dfrac{a*c}{b}\sin(40^\circ)*\cos(15^\circ)} \times \dfrac{c}{c}\\\\ \tan(E) &=& \dfrac{\dfrac{a}{b}*\sin(40^\circ)*\sin(15^\circ)}{\cos(40^\circ)-\dfrac{a}{b}\sin(40^\circ)*\cos(15^\circ)} \\\\ && \boxed{ \dfrac{a}{b} = \dfrac{\sin(65^\circ)} {\sin(40^\circ)} } \\\\ \tan(E) &=& \dfrac{\sin(65^\circ)*\sin(15^\circ)}{\cos(40^\circ)-\sin(65^\circ)*\cos(15^\circ)} \\\\ E &=& -65^\circ~ \text{or}~ \mathbf{E=115^\circ} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline x &=& 320^\circ-(D+E) \\ x &=& 320^\circ-(105^\circ+115^\circ) \\ x &=& 320^\circ-220^\circ \\ \mathbf{x} &=& \mathbf{100^\circ} \\ \hline \end{array}\)

Thank you CPhill !

Find the sum \(1*3 + 3*5 + 5*7 + 7*9 +\ldots\) for the first \(n\) terms.

\(\begin{array}{|rcll|} \hline \mathbf{1*3 + 3*5 + 5*7 + 7*9+ \ldots} &=& \mathbf{\sum \limits_{k=1}^{n} (2k-1)(2k+1)} \\ &=& \sum \limits_{k=1}^{n} (4k^2-1) \\ &=& \sum \limits_{k=1}^{n} 4k^2 - \sum \limits_{k=1}^{n} 1 \\ &=& 4\sum \limits_{k=1}^{n} k^2 - \sum \limits_{k=1}^{n} 1 \\ && \boxed{\sum \limits_{k=1}^{n} 1=n}\\ &=& 4\sum \limits_{k=1}^{n} k^2 - n \\ && \boxed{\sum \limits_{k=1}^{n} k^2=\dfrac{n(n+1)(2n+1)}{6} }\\\\ &=& \dfrac{4n(n+1)(2n+1)}{6} - n \\\\ &=& \dfrac{2n(n+1)(2n+1)}{3} - n \\\\ &=& \dfrac{2n(n+1)(2n+1)}{3} - \dfrac{3n}{3} \\\\ &=& \dfrac{n}{3}\Big( 2(n+1)(2n+1)-3 \Big) \\\\ &=& \dfrac{n}{3}\Big( (2n+2)(2n+1)-3 \Big) \\\\ &=& \dfrac{n}{3}\Big( 4n^2+6n+2-3 \Big) \\\\ \mathbf{1*3 + 3*5 + 5*7 + 7*9+ \ldots} &=& \mathbf{\dfrac{n}{3}\left( 4n^2+6n-1 \right)} \\ \hline \end{array}\)

ABCD is a square with side length x and length DE is 1.
Find the value of x for which the area of the shaded region is 1.

\(\text{Let $D=(0,0)$ } \\ \text{Let $A=(0,x)$ } \\ \text{Let $C=(x,0)$ } \\ \text{Let $E=(1,0)$ } \\ \text{Let $B=(x,x)$ }\)

line AC (Y = mX+b): \(Y =-X+x\)
line EB (Y = mX+b): \(Y =\dfrac{(X-1)x}{x-1}\)

intersection AC-EB: \(Y=-X-x=\dfrac{(X-1)x}{x-1}\)
intersection (\(x_i,y_i\)): \(x_i = \dfrac{x^2}{2x-1}\)  
\(y_i = -x_i+x\)

area:

\(\begin{array}{|rcll|} \hline A &=& [ABC] - \dfrac{x}{2}*x*\dfrac12-\dfrac{1}{2}*x*(x-x_i ) \\ &=& \dfrac{x^2}{2} - \dfrac{x}{2}*x*\dfrac12-\dfrac{1}{2}*x*(x-\dfrac{x^2}{2x-1} ) \\ && \ldots \\ A &=& \dfrac{x^2}{2}*\left( \dfrac{x}{2x-1} - \dfrac12 \right) \\ && \ldots \\ A &=& \dfrac{x^2}{4}*\dfrac{1}{(2x-1)} \quad | \quad \mathbf{A=1} \\ 1 &=& \dfrac{x^2}{4}*\dfrac{1}{(2x-1)} \\ 4(2x-1) &=& x^2 \\ x^2 -8x+4 &=& 0 \\\\ x &=& \dfrac{8\pm\sqrt{64-4*4}}{2} \\ && \ldots \\ \mathbf{x} &=& \mathbf{4+2\sqrt{3}} \qquad x=7.464101615 \\ \hline \end{array}\)