Melody

(3+2√2)^2n-1 + (3-2√2)^2n-1 - 2

\((3+2\sqrt2)^2*n-1 + (3-2\sqrt2)^2*n-1 - 2\\ =n(3+2\sqrt2)^2 + n(3-2\sqrt2)^2-4\\ \)

Is this what you intended to write or do you need brackets anywhere?

Have you tried it?

Here is the fromula

Thanks Heureka,    

Note that my answer is the same as Heureka's    

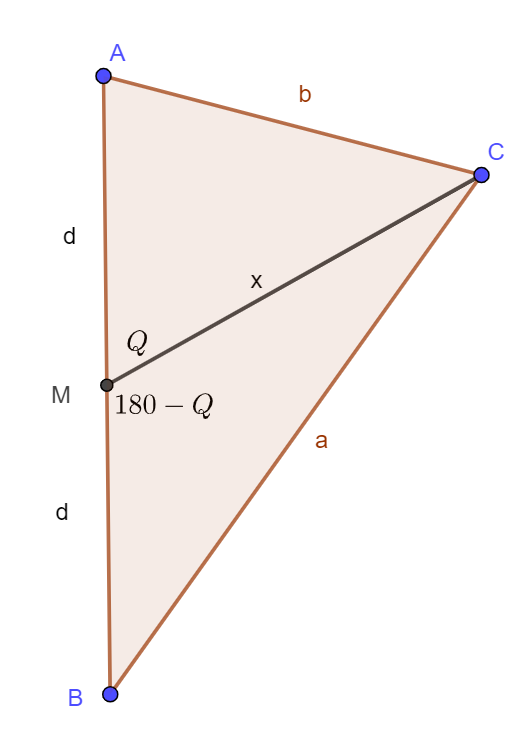
In triangle ABC, show

\(CA^2+CB^2=2CM^2+\frac{AB^2}{2}\)

Consider the triangle as I have drawn it and using Cosine rule.

\(a^2=d^2+x^2-2\;d\:x\;cos(180-Q)\\ a^2=d^2+x^2+2\;d\:x\;cos(Q)\qquad\qquad (1)\\~\\ b^2=d^2+x^2-2\;d\:x\;cos(Q)\qquad\qquad (2)\\ add\\ a^2+b^2=2d^2+2x^2\\ \text{Substituting original notation}\\ CB^2+CA^2=2(\frac{AB}{2})^2+2CM^2\\ CA^2+CB^2=2CM^2+2(\frac{AB^2}{4})\\ CA^2+CB^2=2CM^2+\frac{AB^2}{2}\\\)

okay, so do you understand what Alan has told you?

Thanks Alan :)

The 'tags' button on the bottom right has a drop-down menu.  Off-topic is in there.

Thanks Answer guest.

I have not looked at the answer but asker guest, it is up to you to accept or reject it.

It is polite to comment anyway ... but if you have queries or concerns make sure you voice (or type) them.

This looks promising

ok I have submitted an answer.

See this.