Melody

You have asked this question appropriately, thanks for that,  but you have not said why do you think the original answers are incorrect?  

I have not looked at it but if Heueka, Dragan and Jugoslav all have the same answer I would say it is most likely correct.

They are all respected members.

Hi Maths solver,

I have played with it but I have no idea.   

Is the worked answer given?

let the dimensions be x and y          DRAW PICTURES OF THE RECTANGLES

x * y = ?

decrease each of the sides by 1.  Now we know that

(x-1)(y-1) = ?

expand this and work out the value of  x+y

If you increase the sides by 1 then you have an area of   (x+1)(y+1)

expand this then substitute the known values.

Now you have your answer.

Give it a go and get back with what you have done.   

You can use the quadratic equation to solve this.

\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)

Think about it.  When will this have exactly one solution?

If you want to assume that the children are not identical then you tie the boys together and not you have 4 'children'

they can be arranged in a line in 4! ways.  But either one of the boys can be to the left so we need to double this answer.

4!*2 = 48 ways

Guest is probably telling you that you need to do your own homework.

I have deleted most of your questions.  

Please stop using this as a cheat site. 

People here want to help others, they do not want to do all your homework for you.

Good, I hope it is.

Do not dump all your homework here and expect the rest of the world to do it for you.

So guest, are you going to show some interest or was I only amusing myself?

How about you give the addresses of the previous questions/answers.

there is no point in me giving the same/similar answer as before if you did not understand the first time.

If you do not understand an answer you should quiz the answerer on the original thread.

You can make a new post directing people to the original and you can ask for it to be unlocked if it is locked.

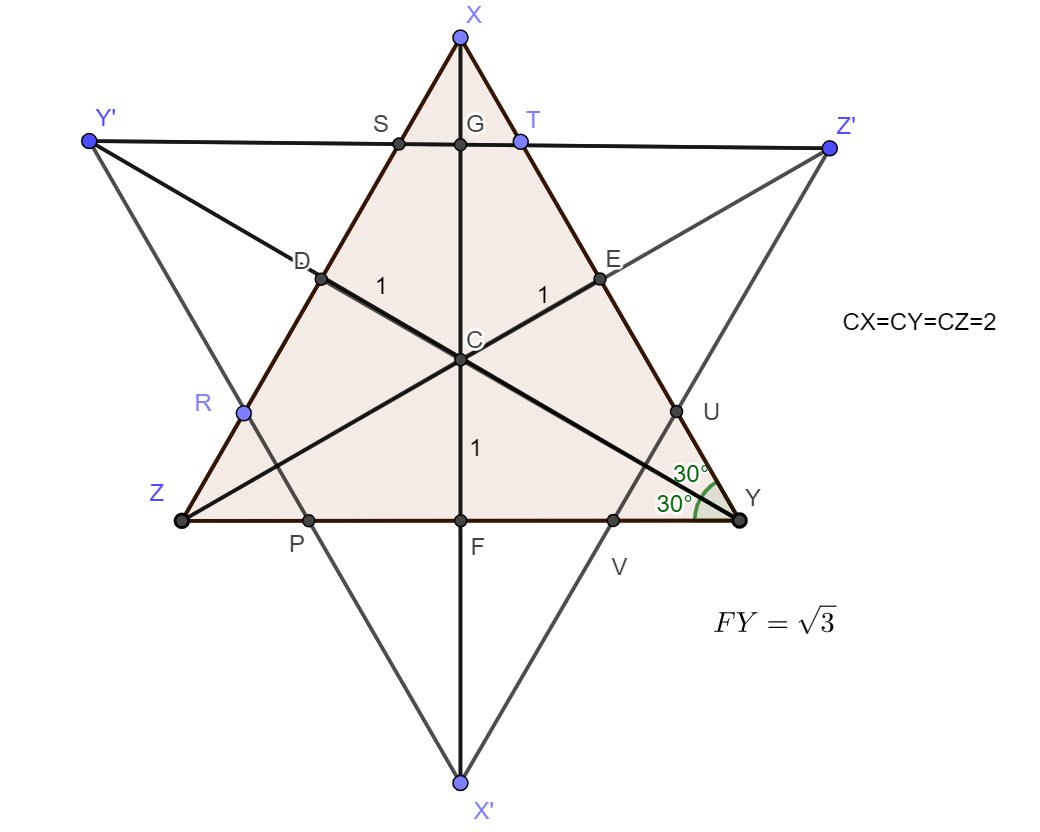
I let GF=1   (just for ease)

CX=2    (30,60,90 triangle)

This means that the sides of the original triangle are   \(2\sqrt3\;units\)

So the area of the original triangle is  

\(Area\;XYZ = \frac{1}{2}*2\sqrt3*2\sqrt3*sin60\\ Area \;XYZ= 6*\frac{\sqrt3}{2}\\Area \;XYZ= 3\sqrt3\;\;u^2\)

CG=4/3

So GX=2 - 4/3 = 2/3

\(tan60=\frac{XG}{GT}\\ \sqrt3=\frac{2}{3*GT}\\ GT=\frac{2}{3\sqrt3}\\ \)

\(\text{Area of }\triangle STX = GT*GX = \frac{2}{3\sqrt3}*\frac{2}{3}\\~\\ \text{Area of }\triangle STX = \frac{4}{9\sqrt3}\\~\\ \text{Area of intersection}=\triangle XYZ-3*\triangle XST\)

 \(Intersection\; area = 3\sqrt3-3*\frac{4\sqrt3}{27}=\frac{27\sqrt3-4\sqrt3}{9}=\frac{23\sqrt3}{9}\\~\\\)

\(\displaystyle \frac{\text{intersection area}}{\text{area of original triangle XYZ}}=\frac{23\sqrt3}{9}\times \frac{1}{3\sqrt3}=\frac{23}{27} \)