Melody

Thanks Gino,

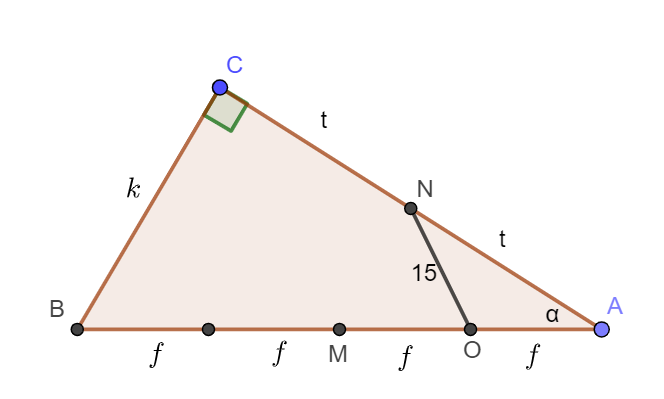
You have done a lot of work there but unfortunately, you did label  O incorrectly.

\(15^2=m^2+t^2-2mt\cdot cos\alpha\\ Cos\alpha = \frac{2t}{4m}=\frac{t}{2m}\\ so\\ 225=m^2+t^2-2mt \cdot \frac{t}{2m}\\ 225=m^2\\ m=15 \)

This means that  the hypotenuse is  60

and the sum of the other 2 sides is  112-60 =52

As guest has already told us very loudly  ,  this is impossible.

So such a triangle cannot exist.

You are criticizing the echo,  but you have not commented on the real post.

Looks like someone has gone to a lot of effort for you.   Now it is your turn to interact with your answerer.

I have no idea.

Would you like to show us Alan?

This question is easy.

Add the first 4 equations together

sum of left = sum of right

 you will have 

p( ...) +q(...) +r( ...) = (...)

factorize and take it from there

Hi Textot,

What you have done looks very impressive.   

I have to think about it some more.  

3 tenths is 36

1 tenth is  12

100%   is  120

3/8*120 = 45

45+36 = 81

120-81  = 39

12*         8

1*2        8

21*        8

2*1        8

*12        7

*21       7

8+8+8+8+7+7 = 46

I counted it logically, with a table, and got 20

You need to use your own logic to check what I have done though.

Take 5,6, and 7 

Now you can add  0 more, or 1 more or 2 more etc right up to all of them.

1 more   7C1 ways

2 more   7C2 ways

etc.

Now if you have any idea what I'm talking about you can finish it easily. 

You got it !!