CPhill

Thanks, heureka....here's my approach....

Using the Law of Cosines we have that

12^2 = (2CD)^2 + 6^2  -  [ 2 * 2CD * 6 ] cos BDA

144 = 4CD^2  + 36 - 24CDcosBDA

108 - 4CD^2  = - 24CDcosBDA

[ 4CD^2 - 108 ] / 24CD  = cos BDA

[CD^2 - 27 ] / 6CD  =cos BDA

Since BDA  and CDA  are supplementary.....-cos BDA  =  cosCDA

Using it again and substituting, we have

9^2 = CD^2 + 6^2  - [ 2 * CD * 6 ] [-cos BDA]

81  = CD^2 + 36 + 12CD  [ CD^2 - 27] / 6CD ]

45 = CD^2 + 2[CD^2 - 27 ]

45 = CD^2 + 2CD^2 - 54

99 = 3CD^2

33 = CD^2

√33 = CD

And  BD  is twice this

So

BD + CD  =  BC  =  √33  + 2√33  =   3√33

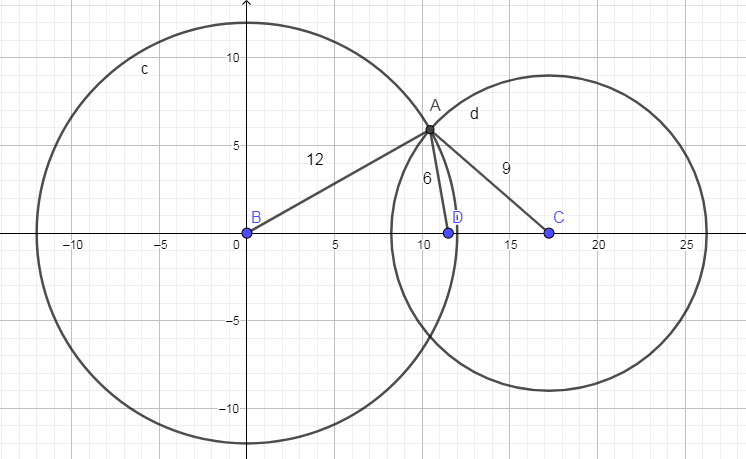
Here's a pic :

Remember that  we cant have any values that make a denominator  =  0

So.... k cannot   =3    because that makes the denominator 0

I don't know where they get  -5/2......this functiion is certainly defined at k  = -5/2

See the graph, here : https://www.desmos.com/calculator/hh4osmk1fc

I've substituted x for k, but the idea is still the same....

For the first function

x^2 - 5x - 64  =2

x^2 - 5x -66 = 0    factor

(x - 11)  ( x + 6)  = 0

The only solution  for the first restriction  is  x  = -6  ⇒ (-6, 2)

For the second function

x^2 + 3x - 38  = 2

x^2 + 3x - 40  =0\

(x + 8) ( x - 5)  = 0

The only solution for the second restriction is  x = 5 ⇒  (5 , 2)

So....two points

This area forms a rectangle with vertices  (0,0), (1.5,1.5), (-1,4)  and (-2.5, 2.5)

The length of one side is  √ [2 * 1.5^2 ] =  1.5√2

And the length of the other side is √ [2 *2.5^2 ]  = 2.5√2

So  the total area  = 1.5√2 * 2.5√2  =  3.75 * 2    =  7 units^2

Here's a pic of the region :  https://www.desmos.com/calculator/zlpwagi3cx

Nice one, hectictar   !!!

2. If f(x)=ax^4-bx^2+x+5 and f(-3)=2, then what is the value of f(3)?

If  f(-3)  = 2, we have

2  = a(-3)^4 - b(-3)^2 - 3 + 5

2  = 81a - 9b + 2

0 = 81a - 9b  

9b  = 81a

b = 9a

f(3)  =  a(3)^4 - (9a)(3)^2 + 3 + 5

f(3)  = 81a - 81a  + 3 + 5

f(3)  = 8

 \( f(x) = \sqrt{\dfrac{x+1}{x-1}}\qquad\qquad\)

\(\qquad\qquad g(x) = \dfrac{\sqrt{x+1}}{\sqrt{x-1}}.\)

If these functions are the same, they have the same domain.....

Notice that the domain of the first function is   (-inf, -1) U (1, inf )

But  the domain of the second function is only (1, inf)......any  negative in the denominator makes this function undefined for the set of real numbers.....

So....these functions are not the same

\(\frac{3x - 7}{x + 1}\)

The domain  will include all real numbers except x  =  -1

So.....

(-inf, -1)   U  (-1, inf )

First one

0 is not in the domain

-1 is not in the domain

-1/2 is not in the domain

The sum of these   is   -3/2

Since AB  = AC, then

Angle ABC  = angle ACB

And since BD = BC

Then Angle BDC  = Angle DCB

But DCB  = ACB

So....triangles   ABC  and  BDC  are similar

Call angle ABC  = 2theta

But since ABC is bisected, then  DBC  is also  = theta

And angle DBC  = angle BAC  = theta

Then...in triangle ABC

Angle ABC + Angle ACB  + Angle BAC  = 180

2theta + 2theta + theta  = 180

5theta  = 180

theta  = 36°=  BAC   = "Angle A "