CPhill

Thanks, tertre....I have a feeling that there is a better geometric way of doing this, but I don't know what it is....

Thanks to Guest for the good answer, too....the Law of Cosines works well!!!!

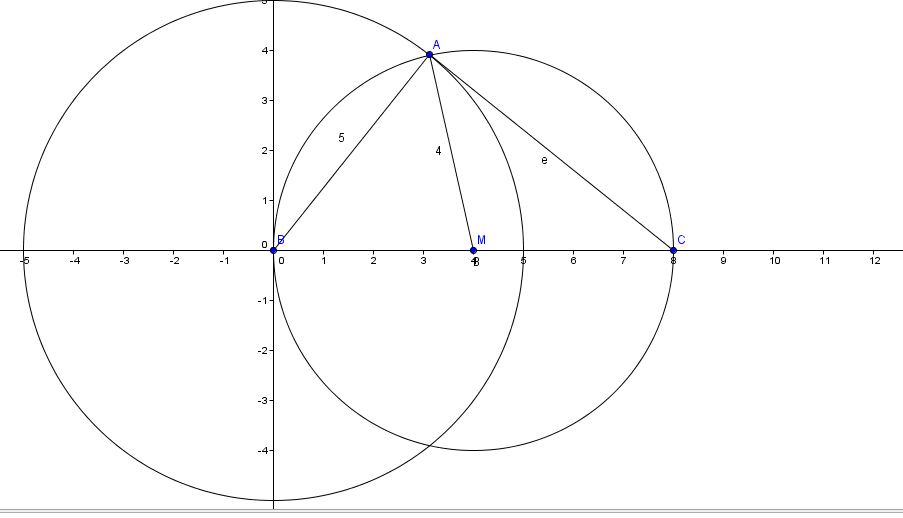
Here's one way to do this, tertre.....but maybe not the most elegant  !!!!

Let B  = (0,0)   C  = (8,0)

Since AM  is a median drawn to BC....then M  is  (4,0)

Now.....construct a circle with a radius of 5 centered at the origin

The equation of this circle is

x^2 + y^2  =  25      (1)

And construct a cirrcle with a radius of 4 centered at M

The equation of this circle is

(x - 4)^2 + y^2 =  16  (2)

Subtract  (2) from (1)   and we have that

x^2  - (x - 4)^2  =  9       simplify

x^2  - x^2 + 8x - 16   = 9

8x  = 25

x  = 25/8

This is the x coordinate of A

To find the y coordinate, we have

(25/8)^2 + y^2  =  25

625/64 + y^2  =  25

y^2   =  25  - 625/64

y^2  =  1600/64 - 625/64

y^2  = 975/64        take th positive root

 y = sqrt (975)/ 8

So  A   =  (25/8, sqrt (975/8)

So....using the distance formula  AC  =

sqrt  [ (8  - 25/8 )*2  + 975/64 ]  =

sqrt [ ( 39^2) / 64 + 975 / 64 ]  =

sqrt (39^2 + 975)  / 8  =

sqrt (2496)  / 8  =

sqrt  (2^6 * 3 * 13)  / 8  =

sqrt (64 * 3 * 13 ) / 8

8sqrt (39)  / 8

sqrt (39)

Here's a pic  :

See the setup below :

Let  A  = (4, 12)

B = (0, 0)

C  = (24, 0)

So......the height of ABC  is 12  and  the base  is 24...so the area  is 12 * 24 / 2  =  144

E  is  ( 14,6)     and D  is  ( 12, 0)

Since AD  is a mediah....then GD  is (1/3)  of AD.....so.....the y coordinate of G  will be  (1/3) the y coordinate of A  = (1/3)(12)  =  4

So  MN  has the equation  y  = 4

And since the y coordinate of E  is 6  and E  is the apex  of ENG...the height of ENG  is

[ y coordinate of E - 4]  =  [ 6 - 4 ]   =  2

And since MN is parallel to BC....then  trinagle AGN  is similar to triangle ADC

And the height of AGN  = 8   and the  height of ADC  = 12

So each dimension of AGN  is 2/3  of ADC

And the base of ADC  = 12

So....the base of AGN  = GN  = (2/3)base of ADC  = (2/3)(12)  =  8

So....the area of ENG  =  (1/2)*GN * height of ENG  = 

(1/2) *  8  *   2  =

8  units^2

Thanks, Mathhemathh!!!....great answer  !!!

f(x)  =  3x + p

g(x)  = px + 4

I think this is supposed to be f(g(x))

f(g(x))  =  3(px + 4) + p   =  3px + 12 + p

So

3px + (12 + p )    = 6x  + q

Equating coefficients, we have

3p   =  6  ⇒    p  =  2

12 +  p  =  q   ⇒  12 + 2  =  q   ⇒  14  =  q

If we interpret this as fg(x), we get that

(3x + p) (px + 4)  =  3px^2 + p^2x + 12x + 4p  =  3px^2 + (p^2 + 12)x + 4p

So

3px^2 + (p^2 + 12)x  + 4p  = 6x + q

Equating coefficients, we have

3p  =  0

p^2 + 12  =  6

4p  = q

But....the first equation  means p  =  0   and the second equation is impossible for any real p....so.....no solution  for fg(x)

(1.5,  -2.3)

(1.5,  6.3)

The distance  is given by :

√ [ 1.2^2  + 3.2^2 ]   =  √ [ 1.44 + 10.24  ]   = √ 11.68  ≈  3.42 miles

Right triangle

Can't see the responses for the drop-down menus, but my best guesses are :

Triangle

Hypotenuse 

Length

3.  What is the coefficient of x in (x^4 + x^3 + x^2 + x + 1)^4?

x^16 + 4 x^15 + 10 x^14 + 20 x^13 + 35 x^12 + 52 x^11 + 68 x^10 + 80 x^9 + 85 x^8 + 80 x^7 + 68 x^6 + 52 x^5 + 35 x^4 + 20 x^3 + 10 x^2 + 4 x + 1

The coefficient  is  4

4.   From above....the  coefficient on the x^3  term  is  20