CPhill

13 degrees  17 minutes 50 seconds

We don't need to worry about the degree conversion..we need to convert the minutes and seconds to decimal degrees

There are 60 minutes to each degree  so we can express this as     17/60  degrees

And there  are  3600 seconds in each degree so we can express this as  50/3600 degrees 

So...adding   D, M ,S  in terms of degrees, we have...

D   +  M     +   S     =

13°  + 17/60° + 50/3600°   =

13.297222°  =   13.297°  (rounded)

BTW, Manuel....here's an app where you can check these conversions :

https://www.rapidtables.com/convert/number/degrees-minutes-seconds-to-degrees.html

However....if you use this fractional adding procedure above.....you shouldn't have much trouble on these!!!

This object  is known  as the frustum  of a right circular cone .

The volume is given by :

pi * height  ( r₂^2 + r₁r₂ + r₁^2 ) / 3

The height is not given but it is the leg of a right triangle  with the other leg  = 12 - 8  = 4

And  the hypotenuse = l  = 10

So  the height  is sqrt (10^2  - 4^2)  =  sqrt (100 - 16)  =  sqrt (84)  = 2sqrt (21)

So the volume is

pi * 2sqrt (21) * [ 12^2  + 8*12 + 8^2 ]  / 3  =

pi * 2sqrt (21) * [ 144 + 96 + 64] / 3  =

pi * 2sqrt (21) *  [ 304] / 3   =

[ (608/3) * sqrt (21) pi  ]    units ^3

Here's a resource that also might help. Manuel :

https://www.mathsisfun.com/sine-cosine-tangent.html

Angle ADB  = 90°

And angle DBA = 71°

So  angle BAH = 90 - 71  =  19°

And angle BEA  = 90°

And angle EAB  = 46°

So  angle ABH = 90 - 46  =  44°

So...in triangle AHB,  angle AHB  =  180  - 19 - 44  = 117°

Here's a pic  :

\( 4(x^4 + 3x^2 + 1)\)  =

4x^$ + 12x^2  + 4

4^2*(2)  + (12)^2 

16*2  + 144

32 + 144

176 

Here are the graphical solution(s) : 

https://www.desmos.com/calculator/r5bmyzfyrx

They occur  at (-2, 5)  and  ( 2, - 3)

I don't really understand what this  " Choose maximum or minimum point first and then a point on the parabola."    has to do with finding the solutions.....(????)

The first graph is the graph of      y  =   6cos(x)

This graph is symmetric about the y axis....so it is even

The second graph  is the grah  of  y  = x^2  - 9

It is also symmetric about the y axis....so  it is also even

This one isn't too bad, tertre  !!!

Note that a multiple of a 3-4-5 right triangle  is a 15-20-25 right triangle....

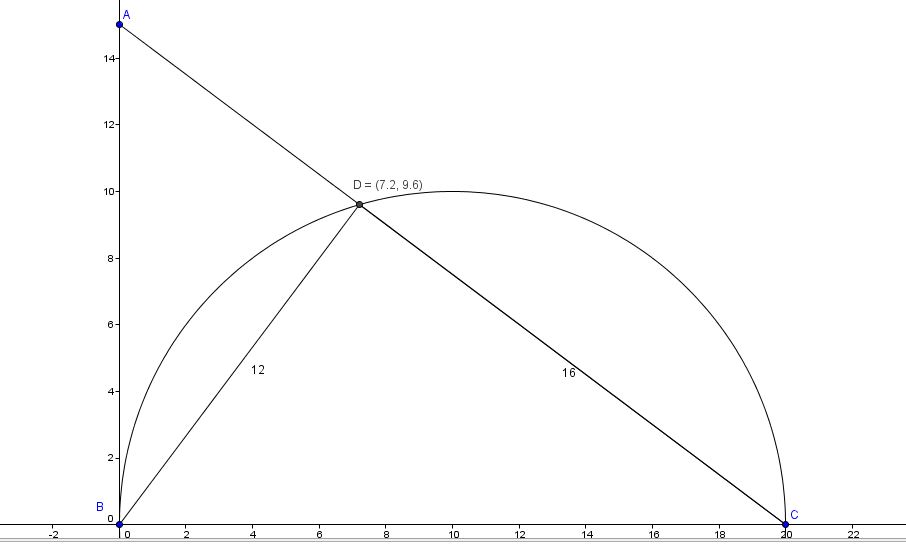
Let B = (0,0)

A= (0,15)

C= (20, 0)

The area of ABC is  (1/2)BC * BA   =  (1/2)(20)(15)  = 150  which is what we need!!!

Let the  circle with the diameter of BC  have the equation (x - 10)^2 + y^2  = 100  (1)

And let the slope of the line containing AD   =  -15/20  = -3/4

And the equation of this line is

y  =( -3/4) x  +  15        or

y = (15 - 3/4)x

Square both sides of this

y^2 =  ( 15  - (3/4)x)^2     (1)

Our objective is to find the x coordinate of the second intersection of AC  and this circle 

Sub (2)  into (1)  and we have

(x - 10)^2  + (15 - (3/4)x)^2  =  100     simplify

x^2 -20x + 100 + 225 - (90/4) x + (9/16) x^2  = 100

x^2 -20x + 225 - (90/4) x  + (9/16)x^2  =  0    multiply through by 16

16x^2 - 320x + 3600 - 360x + 9x^2  =  0

25x^2 - 680x + 3600  =  0

Believe it or not....we can factor this as

(5x - 36 (5x - 100)  = 0

Set  each factor to 0  ans solve for x and we have that

x =36/5    and x  = 20

We already know that  the  second value is an x intersection of the line and the circle

We are interested in the first.... and this is the x coordinate of D

The y coordinate  is 

y   = ( - 3/4) (36/ 5)  + 15

y  =  -108/20 + 15

y  = -27/ 5 + 75/ 5

y = 48/ 5

So.....D  =  ( 36/5, 48/5)

So BD is easy to find  as

sqrt  [  (36/5)^2  + (48/ 5)^2 ]  =  

sqrt [ 36^2 + 48^2] / 25  =

sqrt [ 3600 ]  / 5 =

60 / 5   =

12 units

Note something interesting....that triangle BDC  is  a  12-16-20 right triangle which is another multiple of a 3-4-5 right triangle  !!

Here's a pic of all of this :

Nice, hectictar  !!!!

WolframAlpha will handle this kind of thing easily, Asad

Here is the website  : https://www.wolframalpha.com/input/?i=125+%2B+375&lk=3

BTW.....the result is  :   0.001761234660127750786146537262298337049389923395170376734....