CPhill

\((\sqrt{600} + \sqrt{150} + 4\sqrt{24})/(6\sqrt{32} - 3\sqrt{50} - \sqrt{2})*8 = a\sqrt{b}\)

Let's take this  one term at a  time

sqrt (600) =  sqrt (100 * 6)  = 10sqrt 6

sqrt (150 )  =    sqrt ( 25 *6) = 5sqrt 6

4sqrt (24)  =  4 sqrt ( 4 * 6)  = 4*2 sqrt 6  = 8 sqrt 6

Adding these three terms we get   23 sqrt 6

Multiplying by 8  we get   184 sqrt 6

Now....look at the terms in the  denominator

6sqrt ( 32)  =  6sqrt ( 16 *2)  = 6*4 sqrt ( 2) =  24sqrt 2

3sqrt (50)  =  3 sqrt (25 * 2) = 3*5 sqrt (2)  = 15sqrt 2

sqrt ( 2) = 1 * sqrt (2)

So the denominator =  (24 - 15 - 1) sqrt 2   =  8sqrt 2

So  we have    184 sqrt 6  / ( 8 sqrt 2)  =  (184/8) sqrt 6 /sqrt 2 =  (23)sqrt 3

a + b =   23  +  3 =  26

The time  for the cyclist  to  ride the first segment  is    30 km / (9km / hr) = 30/9 hr = 10/3 hr

Call the  rate that the cyclist must average in the second segment = R

The total time for the second segment =  20  km / R km / hr   =  (20/R) hr

The total distance traveled =   50 km

So

Total Distance  / ( Total Time  ) =   Avg  Rate

So

50  /(10/3  + 20/R)  =  10

50 /  10  =   (10/3 + 20/R)

5 = 10/3 + 20/R

5 - 10/3  = 20/R

5/3 = 20 / R

R = 20 / (5/3)  =  20 * 3/5  =    60 / 5   =   12 km/ hr 

4 ( x + 7)(2-x)  + 4(x + 7) (6-x)   =

4[ 2x + 14 -x^2 - 7x ]  + 4 [ 6x + 42 -x^2 -7x ]  =

4 [ -x^2 -5x + 14 ] +  4 [ -x^2 -x + 42 ]

-4x^2 -20x + 56  - 4x^2 -4x + 168

-8x^2 - 24x  + 224

This is a parabola with the x coordinate of the vertex given by  -b/ (2a)  =  24 / ( 2 *-8)  = 24/ -16  =- 1.5

And  y coordinate of the  vertex is the max =  -8(-1.5)^2  -24(-1.5) + 224 = -18 + 36 + 224  =    242

OK

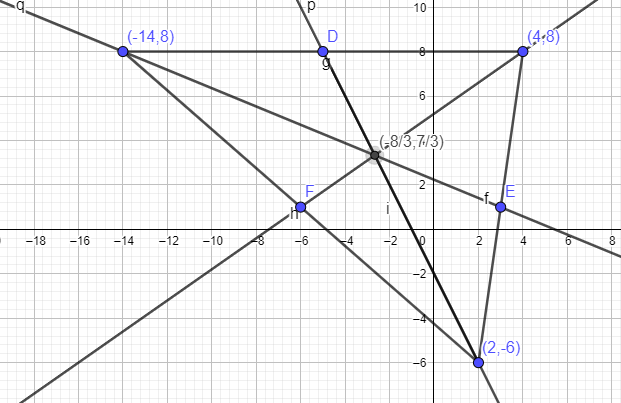
Let C = (-14,8)   and A  =  (4,8)

The midpoint of this  segment is   [  ( 4+ - 14) / 2  ,  ( 8 + 8)/2 ]  =   (-5, 8)

And this  median will pass through B =   (2, -6)

The slope of this median line   =  (-6-8)/(2- - 5)  = -14/7 =- 2

Using the midpoint we can write the equations of the line as

(y - 8) = -2 ( x - -5)

y = -2x -10 + 8

y = -2x -2

Let the midpoint between A and B be [ (4+2 ) /2 ,   (8-6)/2  ] = ( 3, 1)   

And this median will pass through C = ( -14,8)

The slope of this median line is  ( 1-8) / ( 3 - -14)  = -  7/17

And using the midpoint the equation of this median line is

y -1 = - (7/17) ( x - 3)

y = - (7/17)x + 21/17  + 1

y = -(7/17)x + 21/17 + 17/17

y = - (7/17)x  + 38/17

Let the midpoint of  B and C  be  [ ( -14+2)/2 , (-6+8)/2 ]  = (-6, 1)

This median will pass through A = ( 4,8)

The slope of this median =   (1-8)  / ( -6-4)   =  -7 / -10   =  7/10

Using the median the equation of this median line is

y - 8 =  (7/10)(x  -4)

y = (7/10)x - 28/10  + 8

y = (7/10)x -28/10 + 80/10

y = (7/10)x + 52/10  =  .7x  + 5.2

If we set any two of the lines =, we can find the x coordinate of the intersection of the medians

-2x - 2  =  .7x  + 5.2

-2 -5.2  = 2x + .7x

-7.2 = 2.7x

x = -7.2 / 2.7   =  -72/27  =  -8/3

And the y coordinate of the intersection is

-2(-8/3) - 2  =  16/3  - 2  =  16/3 - 9/3 =  7/3

We want to solve this :

-4.9t^2  + 4t - .4 ≥ 8        subtract 8 from both  sides

-4.9t^2 + 4t  - 8.4 ≥  0     multiply through by -1

4.9t^2 - 4t  +  8.4  ≥ 0

Using x for t, look at the graph here :    https://www.desmos.com/calculator/g6yr1y8a7p

Notice that the height is ≥ 8m    between  ≈  .117 sec   and  ≈ .7  sec

Rewrite as  :

1/ (a^3 + 7)  +  a^3 / (a^3 + 7)   =   7

(1 + a^3 ) /  (a^3 + 7)   =  7

Multiply both sides  by a^3 + 7

1 + a^3   = 7 ( a^3 + 7)

1 + a^3  = 7a^3  + 49

1 - 49  = 7a^3  - a^3

-48  =  6a^3

-8  = a^3       take the cube root

-2  = a    ( only real solution)

Assuming  yearly compounding.....

A = 201  ( 1.09)^4   ≈   $283.73

Because   ABFE  = ABFE  and  triangle  BDF  =  triangle  ECF

Then  right triangle ADE   must have the same area as triangle  ABC

Area of triangle BDF  = (1/2)(DB + BA) ( AE)  =   (1/2) (2 + 3)  ( 5) =   12.5

Since triangle  ECF  has the same area we  have that

(1/2)  ( BA )  ( AE  + EC )   =12.5     multiply both sides by 2

(BA) ( AE +  EC)  = 25

(3)   ( 5 + EC)  =  25      divide both sides by 3

EC + 5  = 25/3

EC  =   25/3   - 5

EC  =  25/3  = 15/3   =    10/3

Let us write this in a slightly different  manner  noting that y/y   = 1    and y not equal to  0

y / 3   +  y / y    =  (y + 3)   /  y

Now

y / 3     =   (y + 3) / y    -  y/y

y / 3    =     ( y + 3 - y)  / y

y / 3  =   3 / y            cross-multiply

y^2  = 9      take both roots

y = +3   or   -3

Hope that helps  !!!

Set the first two equations equal

ax + 3   =  x + 5

Let x  = 2

2a  + 3  =   2 + 5

2a  + 3   = 7

2a = 7 - 3

2a  = 4

a = 4/2  = 2

Set the second and third equations equal

x + 5  =  8x + b

Let x  = - 2

-2 + 5  =  8(-2) + b

3  = -16  + b

b = 16 + 3  = 19

So   the sytem that makes these continuous is

y= 2x + 3     ( x > 2)

y = x + 5       [ -2, 2 ]

y  = 8x  + 19    ( x < -2 )

a + b =   2 + 19   =  21

See the graph here : https://www.desmos.com/calculator/ywwaz4mykn