There is only one value of k for which the line x = k intersects the graphs of y = x^2 + 6x + 5 and y = mx + b at two points which are exactly 5 units apart. If the line y = mx + b passes through the point (1, 6), and b ≠ 0, find the equation of the line. Enter your answer in the form "y = mx + b".
For convenience let the vertical line be x = r
Then the point on the parabola that this line intersects = (r , r^2 + 6r + 5)
Call the point on the parabola that the line of interest intersects = (q , q^2 + 6q + 5)
The slope of this line = (6 - [ q^2 + 6q + 5 ]) / ( 1 - q) = ( 1 - q^2 - 6q) / (1 -q) = (q^2 + 6q - 1) / ( q - 1) = m
You have correctly figured out the 6 = m + b
So 6 - m = b
So 6 - (q^2 + 6q - 1) / (q - 1) = b
So [ 6 (q -1) - (q^2 + 6q - 1) ] / (q -1) = b
So [ q^2 + 5 ] / (1 - q) = b
Then the point (0, b) = [ 0 , q^2 + 5 ] / [1 -q)] is on the line
The slope between this point and (1,6) = [ 6 - q^2 - 5 ] / [ (1-q) ] = (1 - q^2] / (1 - q) = 1 + q
Equating slopes
( 1 + q) = ( q^2 + 6q -1) / (q -1)
q^2 - 1 = q^2 + 6q - 1
0 = 6q → q = 0
So the line of interest intersects the parabola at [ 1-q , q^2 + 5 ] = ( 0,5)
So m = slope between (0, 5) and (6, 1) = (6 -5) / (1 -0) = 1
And
b = 5
Our line is y = x + 5 { verify that (1,6) is on this line }
When x = r
Then y = r + 5
And we need the distance between (r , r+5 ) and ( r, r^2 + 6r + 5) to equal 5
So
sqrt [ (r - r)^2 + [ (r +5) - (r^2 + 6r + 5) ]^2 ] = 5
A little tricky to solve....but..solving this for the r we need produces
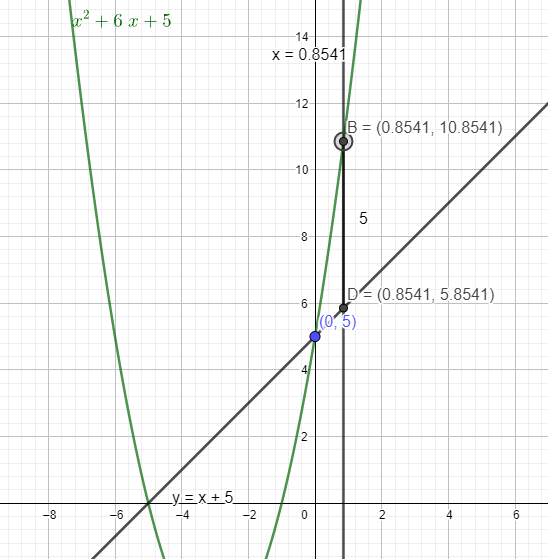
r ≈ .8541
So the vertical line is x = .8541
And y ≈
(.8541)^2 + 6(.8541) + 5 ≈ 10.8541
So ( .8541, 10.8541) = "B" on the graph = the place where the vertical line crosses the parabola
And
(r , r + 5) = ( .85410 , 5.8541) = "B" on the graph where the vertical line intersects y = x + 5
Here's a picture :