CPhill

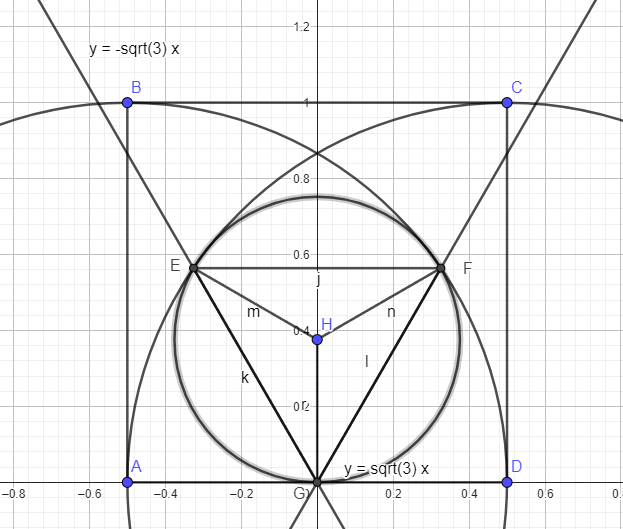
Let the intersection of the circle with the bottom edge of the  square = ( 0 , 0)  = G

Through this point draw lines   y = -sqrt (3) x    and  y = sqrt (3) x

We can  show that this will lead to  the  (approximate)  radius of the  circle

The equation of  one circle is   (x-.5)^2 + y^2   =1

And the intersection of this cirlce with the  line y =sqrt (3) x  can be found as

(x -.5)^2  + (sqrt (3) * x)^2   =1

Solving this for (x,y)  produces ≈ (.3256 , .5641)   = F

And using symmetry  the intersection of the  other circle with the line y = -sqrt (3) x  is

(-.3256 , .5641) = E

The distance between  these   points is  2 (.3256)  ≈ .651  = EF

And the distance between one  of these intersection points  and the intersection of the  circle with the bottom of the  square =   sqrt [ (.3256)^2  + (.5641)^2 ] ≈  .651  = EG  = FG

So we  have an iinscribed equilateral triangle in the  circle with sides ≈  .651

Angle EGF  = 60°  so angle EHF  =120°

Using the Law of Cosines, we can find the  (approximate) radius of the  circle as follows

.651^2  =  2* r^2 -  2*(r^2) cos (120°)

.651^2  = 2r^2 - 2r^2 (-1/2)

.651^2 = 3r^2

r^2  = .651^2 / 3

r = sqrt [ .651^2 / 3 ]  ≈ .3759

I'm sure that someone else may be able to  give a more precise answer  !!!!

              B 45°

                        D

                       75°

  30°       24

A 30°                            75° C

If BAC  = 60°....then because AD is an angle bisector, then angle DAC = 30°

If ABC = 45°

Then angle ACB =  180 - 45 -60 =  75°

And angle ADC  =  180  - 75 -30  =  75°

Triangle ADC is isoceles with AC = AD = 24

Using the  Law of  Sines we  can find BC as follows

BC / sin 60  =  AC / sin 45

BC =  24 sin 60  / sin 45

BC =   ( 24 sqrt (3) / 2) /  (sqrt (2) / 2) =    24 (sqrt 3) / sqrt (2) =  12 sqrt (6)

Area  of ABC  =

(1/2)(AC) ( BC) sin (75°)  =

(1/2) (24)(12sqrt 6) ((1 + sqrt 3) / sqrt 8)  = 

(144 sqrt 6 / sqrt 8) ( 1 + sqrt 3)  

(144) sqrt (3) / 2 * (1 + sqrt 3) =

72 sqrt 3  ( 1 + sqrt 3)  =

216 + 72 sqrt 3 

Probably an infinite  number

I found these   (3, 4) , (11, 26)  , (39, 94)  and  (-3, -4) , (-11, -26), (-39 -94) 

x^2-5x+5 = -4x+7   rearramge as

x^2 - x - 2  =  0        factor as

(x - 2) ( x +1) =  0

The roots   are  2 and  -1

Absolute  value difference  of these  roots =  abs ( 2 - - 1)  = abs (3)  =  3

( x + y)  =54

(x + y)^2  = 54^2  =  2916

Let P =  ( x ,12)

Using the square of the  distance  formula.... P is 10 units from (2,5)....so....

10^2 = ( 2 - x)^2 + ( 12 - 5)^2

100 = x^2 -4x + 4  + 49      simplify and rearrange as 

x^2  -4x + 4 = 51

(x - 2)^2  = 51     take the  positive  root

x - 2  =  sqrt (51)

x =   2 + sqrt (51)

P = (2 + sqrt (51) , 12)

Distance from  the  origin =    sqrt [  ( 2 + sqrt (51))^2  + 12^2  ] =

n =  sqrt  [  4 + 4sqrt (51) + 51 + 144 ]  =

sqrt [ 199 + 4sqrt (47) ]     ≈ 15.09 

x^2+y^2=14x+48y-8x-26y+16   rearrange as

x^2 -6x + y^2 -22y  = 16   complete the square on x, y

x^2  - 6x + 9  + y^2 -22y + 121  =  16 + 9 + 121

(x - 3)^2  + (y -11)^2 = 146

This is a  circle centered at (3, 11)  with a radius  of sqrt (146)

The minimum value of y =   11 - sqrt (146) ≈   -1.083

Angle XOZ = 360 - 124 -92 =  144°

Angle XYZ is a  circumscribed angle  subtending the same arc as  central  angle XOZ

So...its measure  is 1/2 angle XOZ =  (1/2) * 144 =  72°

% discount =   amt off original  price / original price

Cost per lb.  =   $2 / 4 lbs  =  .50 / lb.  =  50 cents per pound

You should be able to answer now