CPhill

We can find an equation of the  line through B and  C

The slope of this line is  [ 2 - - 8 ] / [ -3 -1 ] =  10  / -4 =  -5/2

The equation of  the line through A will have a negative reciprocal slope =  2/5

So.....the equation of this  line is

y = (2/5)(x-2) + 3

y = (2/5)x - 4/5 + 3

y = (2/5)x +11/5

When x =  0  ,  y =  11/5  =  2.2

15 + 2.75x =  28.75          where x =  the number of  beads purchased

See the following :

We can find the inradius of  the triangle shown

The triangle is  isosceles with equal sides of  sqrt (3^2 + 3^2)  = sqrt (18)  = 3sqrt (2) and the remaining  side of 6

Area of triangle =  (1/2) (6) (3)  = 9

Semiperimeter =   ( 2 * 3 sqrt 2  + 6)   / 2 =  3sqrt (2) + 3

Inradius =  Area / semi-perimeter  =   9 / ( 3sqrt (2) + 3)  =  3 / ( sqrt (2) + 1) =  radius of  sphere

Volume of sphere / Volume of  cone  =  (4/3) pi * ( 3 / [sqrt (2) + 1])^3 / [ (1/3) pi  (3^2) * 3 ] =

4 / [ sqrt (2) + 1 ] ^3   ≈   .284 

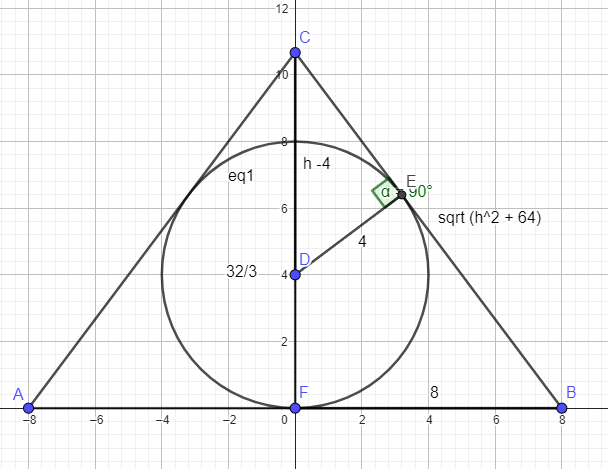
Draw a line from  the  top of the  cone perpendicular to  its  base.....this is the  height  of  the  cone = CF =  h

This forms a  right triangle  with one leg = FB =  8   and the  hypotenuse = BC = sqrt (h^2 + 8^2) = sqrt (h^2 +64)

Next draw a line from the  center of the  sphere perpendicular to  the  side  of the  cone

This forms a right triangle similar to  the  first  one with a leg DE =  4 and  a  hypotenuse=  DC  = h - 4

By similar triangles  

DE / DC   =  FB / BC

4 / (h - 4)  =  8 / sqrt ( h^2 + 64)  cross-multiply

4sqrt (h^2 + 64)  =  8 (h-4)   

sqrt ( h^2 + 64)  = 2(h - 4)   square both sides

h^2 +  64 =  4 ( h^2 - 8h + 16)

h^2 + 64  =  4h^2 - 32h + 64

3h^2 - 32h =  0

h ( 3h - 32) = 0

Setting the second factor =  0

3h - 32  = 0

3h = 32

h = 32/ 3 in  ≈  10.7 in

Simplify as

x^2 + (k - 9)x + 16

This will be the square of a  binomial when the discriminant = 0

So

(k - 9)^2  - 4 (1) (16)  = 0

(k - 9)^2 - 64  = 0

(k - 9)^2  =  64       take  both roots

k - 9 =  8       or   k - 9 =  -8

k = 17                    k =  1

Their sum  =   18

The three inequalities form  a  right triangle with  sides  of 1,1, and 2

By the Pythagorean Theorem, the longest side  is    sqrt (1^2  + 1^2) =  sqrt (2)  = 1sqrt (2)

a = 1   b  =2

a + b  =  3

The intersection  points of the  lines  forming the  vertices of the triangle   are (2,-3) , (-1.5, .5) and (2,4)

This is a right triangle with the hypotenuse on the line  x = 2

The cicumcenter  occurs at the midpoint of the  hypotenuse  = (2, .5)

1/ (a - 1)  +  1/ (b - 1)  =     (a + b - 2)  / ( ab - (a + b)  + 1)

Rearrange the equation  as

3x^2 -11x  - 7  =  0

The sum of the  roots =  a + b =  11/3

The product of the  roots =   ab  =  (-7) / 3

Then  we have   1/ (a - 1)  + 1 /(b - 1)  =   [ 11/3 - 2 ] / [ -7/3 - 11/3 + 1] =

[ 11/3 - 6/3 ]  /  [ -18/3 + 1 ]  =

[ 5/3 ]  /  [ -6 + 1 ]  =

(5/3) / (-5)  = 

5 / -15  =

-1/3

Rearrange as   

x^2  - 8x + t =  0

Possible factors 

                                    roots         t

(x - 7) ( x  - 1)              1 , 7          7  

(x - 2) ( x - 6)               2, 6         12

(x - 3) ( x - 5)               3, 5         15

(x - 4) (x - 4)                  4           16

                                                  ___

                                                    50 =  sum of t's   

Average of t's  =  50  / 4 =   12.5

Not totally sure about this one......!!!

To have two positive real roots,  -( 2q - 9) / q  must be > 0   and  (q - 8) / q  must be > 0

-(2q - 9) / q >  0                       (q - 8) / q >  0

9 - 2q > 0                                   q - 8  >  0

9 > 2q                                         q >  8

q < 9/2 

No solutions exist  for  q  since these intervals  do  not  intersect