CPhill

Area =  (1/2) AB * BC * sin (ABC)  =

(1/2) (6)(8) * sqrt (2) / 2 =

12 sqrt (2)

This is a right triangle

Area = (1/2) (15) (20)  =  150

The shortest altitude is  drawn  to  the  longest side

Area =  (1/2) (25) (altitude)

150 = (1/2) (25) (altitude)

300 = 25 * altitude

300 / 25 =   12  = altitude

Triangle PUQ is similar to  triangle TUS

ST = 3 / (2 + 3) * SR  =  (  3/5) * (20) =  12

So ST / PQ = 12 / 20  =  3/ 5

Then  the altitude of PUQ =  QV

And the altitude of TUS = RV

So  RV  /  QV =  3 / 5

And QV / QR =  QV / ( QV + RV)  =   5 / ( 5 + 3) =  5 / 8

So QV = (5/8)QR

And triangle  QUV is similar to  triangle QSR

So

UV / QV =  SR / QR 

UV /  (5/8)QR = 20 / QR

UV  / (5/8) = 20

UV  = (5/8) (20)    =  12.5

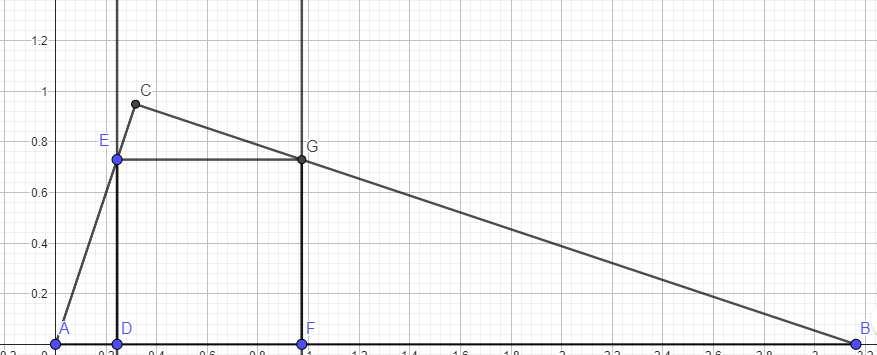
Using similar triangles (twice)....let AD = x  and  side of the square=  s

AB / AE =  BC / DE

sqrt (10)  / sqrt (s^2 + x^2)  =  3 / s

10 / (s^2 + x^2)  = 9 / s^2

10s^2 = 9s^2 + 9x^2

s^2 = 9x^2

s = 3x    → x = s/3

And

AC / FG  = AB / BG

1 / s  =  sqrt (10)  / sqrt [ (sqrt 10 - 4x)^2 + s^2 ]

1/s^2 =  10 / [ (sqrt 10 - (4/3)s)^2 + s^2 ]

(sqrt 10 - (4/3)s )^2  + s^2  =  10s^2

9s^2 =  (sqrt 10 - (4/3)s)^2

9s^2  = 10 - (8sqrt10)s/3 + 16s^2/9

(65/9)s^2 - (8/3)sqrt (10)s - 10 = 0

Solving this for  s produces   

s = (3/13)sqrt (10)  =   sqrt (90) / 13

Area of the  square =  90 / 169

It will  (theoretically) travel

12 / ( 1 - .7)  =   12 / (3/10) =  (12 * 10) / 3  =   40 ft

However....if we set the sum of an infinite geometric series to 40

12 [ 1 - .7^r ] / [ 1 - .7 ]   =  40

12 [ 1 - .7^r ] / .3  = 40

12 [ 1 - .7^r ] =  12

1 - .7^r  =  1

-.7^r  = 0         

Which means that the number of times  (r) that it takes to get the swing to  stop is not determinable......however, with friction involved it will eventually stop

(-2x + 5)  / 7    + ( 3x - 1) / 2    simplify

[ 2 (-2x + 5)  + 7 ( 3x - 1) ] / [ 7 * 2 ]   =

[ -4x + 10  + 21x  - 7 ]  / 14

[17x + 3 ]  / 14

So

[17x + 3 ] / 14  = 0           and               [ 17x + 3 ] / 14   =1

x = -3/17                                                17x + 3 =  14

                                                               17x  =  11

                                                                  x =  11/17

The real numbers fall into  the  interval  [ -3/17 , 11/17 ]

3 meters =  3 x 100 centimeters = 300 centimeters

70 centimeters  = 70 centimeters

3 decimeters =  3 x 10 centimeters  = 30 centimeters

(300 + 70 + 30)  =    400 centimeters

Nope

For them to trigger again after 360 seconds,  56 must be a divisor of 180  (but , it isn't)

They will trigger again in  

56 =  2^3 * 7

180  = 2^2 * 3^2 * 5

2^3 * 7 * 3^2 * 5  =    2520 seconds  = 42 minutes

a + b + c  = 60

(a - 1) = N    →  a  = N + 1

(b + 2)  = N  →  b =  N - 2

3c  = N        →   c =  N /  3

(N + 1) + (N - 2) + N / 3  = 60

(7/3)N  =  61

N = (61 * 3)  / 7 =   183 / 7

a^2b^3  = 33/27     (1)

ab^3  = 27/4           (2)

Divide (1) by (2)

a = (33/27) / (27/4)  =   44 / 243

Using (2)

(44/243) * b^3  = 27/4

b^3 =  (27/4) / ( 44/243)   = 6561  /176

b = ∛ [ 6561 / 176 ]