CPhill

h(x)  is a polynomial and is  continuous for al real  numbers x

f(x)  is a rational  function and is continuous everywhere except at x  =  7

y = 2x^2

y = x + c

Set the functions equal 

2x^2   = x + c

2x^2 - x -  c =  0

To find one  point  of intersection set the discriminant  = 0  and solve for  c

(1)^2  - 4(2)(-c)  = 0

1 + 8c =  0

1 = -8c

c = - 1/8

Let the number of "8" slips we need to  add = N

So

3 ( 8 / (10 + N) )   +   8 ( 2+ N) / (10 + N )  =  4       simplify

[ 24 + 16 + 8N ]  / (10 + N)  = 4

[ 40 + 8N ] =  4 (10 + N)

40 + 8N  =  40 + 4N

8N = 4N

(8- 4) N = 0

4N  = 0

N =  0         (we don't need to  add any !!! )

Proof   :   

Expected value =  Outcome * Probability  =   3 (8/10)  + 8(2/10)  =  [ 24 + 16 ] / 10  =  40 / 10    = 4

Expected value  = Outcome * probability

So   (3) (8/17)  +( 8 )(9/17)  =    [24 + 72 ] / 17  =  96 / 17 ≈   5.6

The ways to get to  (1,1)  from (0,0)  =  C(2,1)  = 2

Ways to get to *2,2) from (0,0) =    C(4,2)  = 6

So .....ways to  get from  (2,2) from (0,0)  without going through (1,1) =  6 - 2 =  4

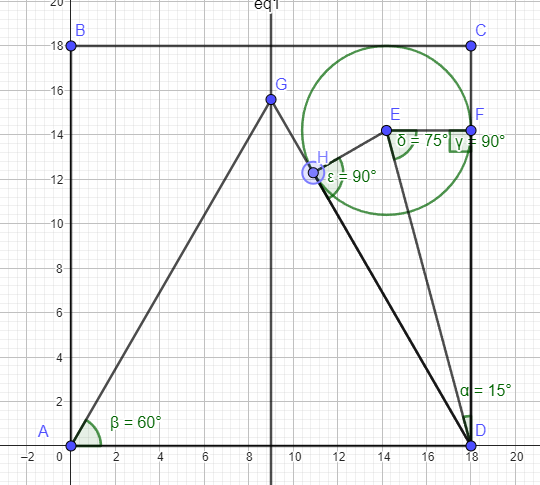
EF  = radius = EH =  9 -sqrt (27)  =  9 -3 sqrt (3)  = r

FD = HD

Angles EFD = EHD = 90

So  by SAS, triangle EFD  congruent to  triangle EHD

Angle HDF  = 30

ED bisects this angle

Angle EDF =15    angle FED =75

Let FD = x

By the Law of Sines

r / sin (15)  = x / sin (75)

 [ 9 -sqrt (27) ] / sin (15) = x / sin (75)

[ 9 -sqrt (27) ] * sin 75 / sin 15  =  x                     (sin 75  = cos 15)

[ 9 -sqrt (27) ] * (cos 15) / (sin 15) =  x

[ 9 - sqrt (27) ] * cot (15) =  x

[9 - sqrt (27) ] * cot (30/2)  = x

[ 9 -sqrt (27)] *  [ 1 + cos 30 ] / sin 30 =  x

[9 -sqrt (27) ] * [ 1 + sqrt (3) / 2 ] / [ 1/2 ]  = x

[9 - 3 sqrt (3)] * [ 2 + sqrt (3)] = x

[ 18 - 6sqrt (3) + 9sqrt (3)  - 9   =  x

[ 9 + 3sqrt (3) ]  = x =  FD

Side of square  =  CF + FD =     radius of circle + x   =    [ 9 - 3sqrt (3) ] +  [ 9 + 3sqrt (3) ]   =   18

\( A(t) = 3 - 5t^3*srqt(t) + 4 + 2^t. Find A(2) - A(1) \)

A(2)  = 3 - 5(2)^3 * sqrt (2) + 4 + 2^2  =   11 - 40sqrt (2)

A (1) =  3 - 5(1)^2*sqrt (1) + 4 + 2^1   =     4

A(2) - A(1)  =   7 - 40sqrt (2)  

We can write

2 ( 1 + 2 + 3 + 4 +......+ 670 + 671)                2

____________________________   =       ____

3 ( 1 + 2 + 3 + 4 +.......+670 + 671)                3

No circle shown  but I assume that  P,Q,R,S are in order  ????

We just need to   convert  radians to  degrees  using conversion  factor    180 /  pi

Note   (x, y)  =  (r * cos (angle measure)  , r * sin (angle measure) )   ,   r = 1 in this  case

2 *  180 / pi ≈  114.6°        point   ≈  ( cos 114.6° , sin 114.6°)  ≈  (-.42 , .91)       =     P

-.5 * 180 / pi  ≈ -28.6°  ≈  360 - 28.6  ≈  331.4°        point ≈ (cos 331.4°, sin 331.4°) ≈ (.88 , -.48)     =  S

10 * 180 / pi  ≈  573° ≈  (573 - 360) ≈   213°         point  ≈  (cos 213° , sin 213°) ≈ (-.84,-.54)  =   R

-3 * 180 / pi  ≈  -171.9° ≈ (360 - 171.9) ≈  188.1°        point  ≈ (cos 188.1° , sin 188.1°) ≈ (-.99, -.14)  =  Q

\( \frac{4x - 1}{5x + 2} + \frac{2x + 3}{x} \)

3 = (4x -1) / (5x + 2)  +  (2x + 3) / x

3=   [(4x -1)(x) ]  + (5x + 2)(2x + 3) ]  /  [ (5x + 2) (x) ]

3 [ (5x +2) x ]=   14x^2 + 18x + 6

15x^2 +6x  =  14x^2 + 18x + 6

x^2 - 12x - 6  =  0

x^2 - 12x  + 36 =  6 + 36

(x - 6)^2  = 42

x - 6 =    ± sqrt (42)

x = 6 ± sqrt (42)