CPhill

Draw OX = sqrt (3)  = OP 

Since QR  is a tangent  meeting the circle at X , then angle OXR = 90

And since the triangle is equilateral, then angle PRQ  = 60

So triangle ORX   is a 30 -60 -90 right triangle

So XR  =  OX /sqrt 3  =   sqrt (3) / (sqrt (3)    = 1

OR = 2

PR  = OR + OP  =   2 + sqrt (3)  =  QR

QR  -  XR  = QX  

2 + sqrt 3  -  1  =  QX  =      1  + sqrt 3

( f ° g) x = (g ° f) x

3(3x + c) - 4 = 3(3x - 4) + c

9x + 3c - 4 = 9x - 12 + c

3c - 4 = -12 + c

2c  =  -8

c = -8 / 2  =    -4

[PR^2 - QR^2 - PQ^2 ] / [- 2 (QR * PQ] = cos PQR

[23^2 -25^2 - 18^2 ] / [ -2 (25 * 18) ] = cos PQR  = 7/15

PM^2  =   QM^2 + QP^2  - 2 (QM * QP) * cos PQR

PM^2 = 12.5^2 + 18^2 - 2(12.5 * 18)* (7/15)

PM = sqrt (270.25) ≈  16.44

f (f(x)) =  p ( px + q) + q =  p^2x + pq + q

f(f(f(x)))  =   p ( p^2x + pq+ q) + q =   p^3x + p^2q + pq + q

So

p^3x  + p^2q + pq + q =  64x - 63x -105 + 278

p^3x  + p^2q + pq  + q = x + 173

Equating terms

p^3  = 1        so  p  =1

And

q ( p^2 + p + 1)  =  173

q  (1^2  + 1 + 1)   = 173

q (3) = 173

q =173/3

p + q =   1 + 173/3  =   176 / 3

\($x^3 y^2 - x^2 y^2 - xy^4 + xy^3 \ge 0 and 0 \le x \le y$\)

This area (in the blue)  is unbounded 

See here :  https://www.desmos.com/calculator/hvtmevyg4f

Let O  be the center of the square

Let M  be the top right vertex of the  square

Let N be the rightmost vertex of the hexagon  and P  be the top right vertex of the  hexagon

Triangle  PON is equilateral  so   PN =  ON  =  1

OM  =  (1/2) diagonal of square =   S /sqrt 2       where S is the side of the square 

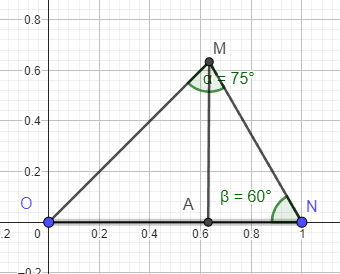
Angle  OMN  = 75°     Angle MON =  45°    Angle MNO = 60° 

Using the Law of Sines

sin (OMN) / 1  =  sin MNO / (S/sqrt 2)

sin (75) /1 =  sin (60)/ (S/ sqrt 2)

S / sqrt (2) =  sin 60 / sin 75

S =    sqrt (2) sin (60) / sin (75) 

S = sqrt (2) (sqrt (3) / 2) /  ( sin (45 + 30)

S = sqrt (6) / (2 (sin 45cos 30  + cos 45 sin 30) )

S =  sqrt (6) / ( 2 ( sqrt (2)/2 * sqrt (3)/2  + sqrt(2/2 )(1/2) )

S =  sqrt (6) / (2 (sqrt (6) /4  + sqrt (2)  / 4)) 

S = sqrt (6) / [ (sqrt (6) + sqrt (2)) / 2

S = 2 sqrt (6) / (sqrt 6 + sqrt 2) 

S = 2 sqrt (6) ( sqrt 6 - sqrt 2) / ( 6-2)

S =  (12 - 2sqrt (12)) /4

S =  3 - 2sqrt (4) sqrt (3) / 4

S =  3 - 2*2 * sqrt (3) / 4

S = 3 - 4sqrt (3) / 4

S =  3 - sqrt (3)  ≈  1.27

Here's a pic  (AM =  1/2 the side of the square ≈  .63 )

1a  + 2  = 2b + 1

1 =  2b - a                                            

Let a =  5 , b = 3         

12₅ =  21₃

1(5) + 2 =   2(3) + 1

7  =  7

\(P_1 P_2 + P_2 P_3 + P_3 P_4 + \dots + P_9 P_{10} + P_{10} P_1 \)

This is just the perimemter  of a decagon

The length of one side can be  found as     radius/2 ( -1 + sqrt (5))

The perimeter  is    10 (1/2) ( -1 + sqrt 5)  =    5 ( -1 + sqrt 5) ≈  6.18

The area is 1/4 of the circle's total area

60pi =   (1/4) pi r^2           divide out pi      multipy through by 4

240  =  r^2

sqrt (240) =  r   = 4sqrt (15)

4 x 2  rectangle at the center = 8

Two triangles at top / bottom with bases of 2 and heights of 1  =  2

Two triangle at left / right  with bases of 5 and  heights of 2  =  10

Total area =   8 + 2 + 10  =   20