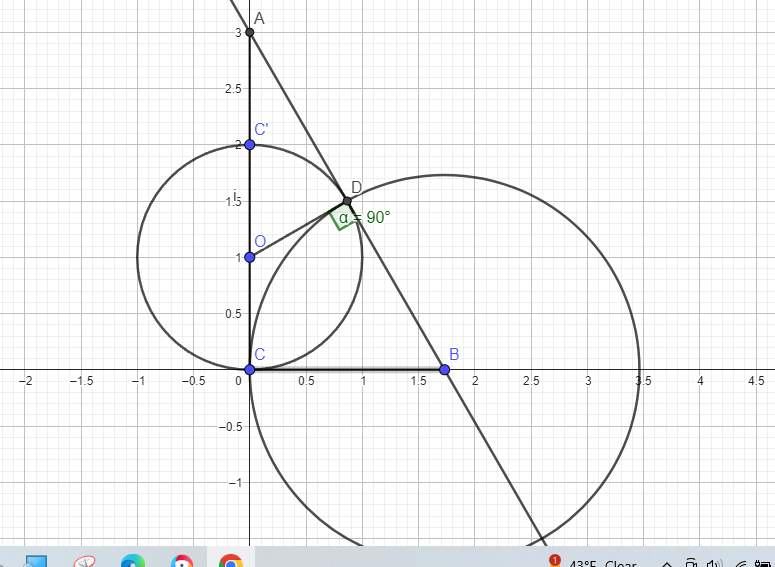
Construct a semicircle with a radius of 1 at O = (0,1)
The equation of this circle is x^2 + (y-1)^2 = 1 → x^2 + y^2 - 2y = 0 (1)
Constuct another circle with a radius of sqrt 3 at B = (sqrt 3,0)
The equation of this circle is ( x - sqt 3)^2 + y^2 = 3 ⇒ x^2 -2sqrt (3)x + 3 + y^2 = 3 →
x^2 -2sqrt(3)x + y^2 = 0 (2)
These circles will intersect at D
To find the D, set the equations of the circles equal
x^2 + y^2 -2y = x^2 + y^2 - 2sqrt (3)x
y = sqrt (3)x sub this value for y back into (2) to find the x coordinate of D
x^2 - 2sqrt (3)x + (sqrt (3) x)^2 = 0
x^2 -sqrt (12 )x + 3x^2 = 0
4x^2 - sqrt (12)x = 0
x ( 4x - sqrt (12)) = 0
4x -sqrt (12) = 0
4x - 2sqrt (3) = 0
4x = 2sqrt (3)
x = sqrt (3) / 2 = the x coordinate of D
y= sqrt (3) * (sqrt (3)) / 2 = 3/2
So D = ( sqrt (3)/2 , 3/2)
The slope of a line through OD = (3/2 - 1) / (sqrt (3)/2 - 0) = (1/2)/(sqrt ((3)/2) = 1/sqrt (3)
The line through BD will be perpendicular to the line through OD so its slope = - sqrt (3)
The equation of the line through BD is
y= (-sqrt (3)) ( x -sqrt (3))
To find the y coordinate of A
When x = 0 , y = 3
So A= (0,3)
And AB = sqrt [ (sqrt (3))^2 + 3^2 ] = sqrt [ 3 + 9 ] = sqrt [12] = 2sqrt (3) ≈ 3.46


