CPhill

A

                X

                         5

B            15                 C

If BXA = 90  then BXC =  90

So triangle  BXC is  right 

So

BC^2  = BX^2 + XC^2

15^2  = BX^2 + 5^2

15^2 - 5^2 = BX^2

200 = BX^2

BX  = sqrt (200)   =  10sqrt(2)

\(a^3 - \dfrac{1}{a^3}$ if $a - \dfrac{1}{a} = 0 \)

a^3 - 1/a^3  = ( a  - 1/a) ( a^2 + 1 +1/a^2)  =  (0)(a^2 + 1 + 1/a^2)   =  0

                 45 B 45

A 45              D                    45 C

The triangle is  isosceles  AB = BC =  12/2 = 6

Angle ABC  = 90

So....Angle ABD = 45

So BD = AD =  6

Area ABD =  (1/2) (AD) ( BD)  = (1/2) (6)(6)  =  18

We can set this  up in a  convenient fashion  to make the math a little easier

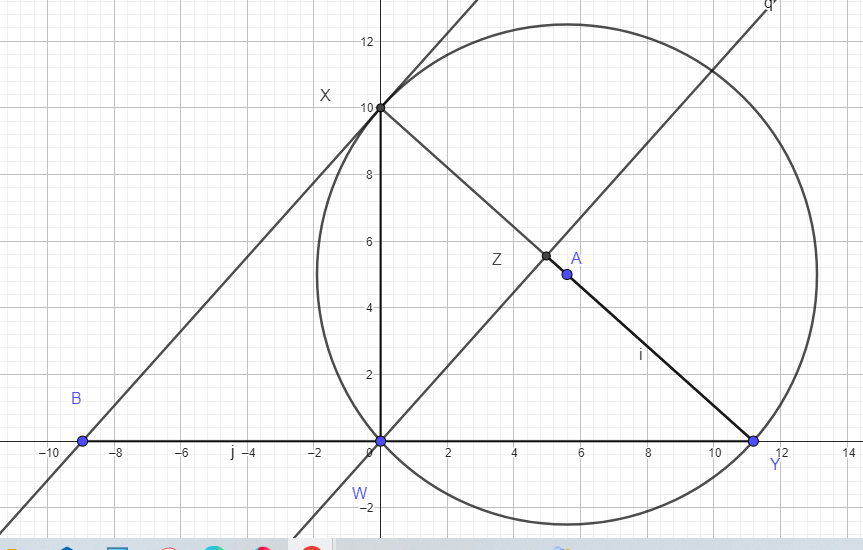
Let W = (0,0)

X = (0,10)

Let WXY  be a right triangle such that

Let XY  be the hypotenuse

XY = 15  WX = 10

WY =  sqrt (15^2 - 10^2)  =  sqrt (125)  =  5sqrt (5)

Y = (5sqrt (5) , 0)

A is  the circumcenter  = (5sqrt(5)  /2 , 5) =  (sqrt 125) / 2 , 5)

The equation of the circumcircle is (x - sqrt (125)/2)^2 + (y -5)^2  = 7.5^2

The slope   of XY  =  -10/ [5sqrt (5)] =  -2 / [sqrt (5) ]

The slope of the tangent line to the circumcircle =  sqrt (5) / 2

The equation of the  tangent line = y =[sqrt (5) / 2] x + 10

The x intercept of this  line can be  found as

0 = (sqrt (5) / 2) x  + 10

-10 = [sqrt (5) / 2] x

x = -20/sqrt (5) =  -4sqrt (5)

B = (-4sqrt (5) , 0 )

BY = 4sqrt (5) + 5sqrt (5)  = 9sqrt (5)

Because WZ is parallele to BX ,  triangles  XBY  and ZWY  are similar

WY / BY  = ZY / XY

(5sqrt (5)) / (9sqrt (5) ] =  ZY/ 15

(5/9) = YZ /15

YZ  = 15 (5/9)  = 75/9  =  25/3

For a hexagon, the area = 6 (1/2) (side)^2 *sqrt (3) /2

3/2  = 6 (1/2)(side)^2 sqrt (3) / 2

3/2 = 3side^2 sqrt (3) /2

1 = side^2 *sqrt (3)

1/sqrt 3 = side ^2

side =  sqrt  [ 1 /sqrt 3 ] ≈ .76

x^2 + 19x + 5  = 0

a^2 + a^3  

b^2 + b^3  

Sum of these roots =     (a^2 + b^2)  + (a^3 + b^3)  =   (a^2 + b^2)  + (a + b)  (a^2 + b^2 - ab)

Also

a^2 + a^3  = a^2(a + 1)        (1)

b^2 + b^3 =  b^2 ( b + 1)      (2)

Product of (1) , (2) = product of these  roots =  a^2*b^2* (a + 1) (b + 1)   =   (ab)^2 ( ab + (a + b)  + 1)

Product of roots in    x^2 + 19x + 5 = 0

ab  = 5

2ab = 10

Sum of roots =   a + b =   -19

Square both sides

a^2 + 2ab + b^2  =  361

a^2 + b^2 = 361  - 2ab

a^2 +  b^2  = 361 - 10

a^2 + b^2 = 351

Sum of roots  in our quadratic = 

(a^2 + b^2)  + (a + b) ( a^2 + b^2 - ab)  =

(351) + (-19) ( 351 - 5)  = -6223

Product of  roots  in our quadratic = 

(ab)^2 ( ab + (a + b) + 1)  =

(5)^2 ( 5  -19 + 1) =

(25) ( -13)  = 

-325

The quadratic is

x^2 + 6223x - 325

Angle OCD = 45

Angle COD  = 90

So....Angle ODC = 45

So triangle DCO  is 45  - 45 - 90

So  OD  = 10/sqrt 2  = OC  =  5sqrt 2

Area of triangle DCO   = (1/2) (5sqrt 2)(5sqrt 2)   = 25

Height of triangle DCO can be found as

25  = (1/2)CD * height

50 = 10 * height

50/10 =  height   = 5

Triangle ABO  similar to Triangle DCO

And the scale factor from triangle ABO  to Triangle DCO   = 4/10 =  2/5

So the height of triangle ABO  = (2/5) (height of tragle DCO)  = (2/5) (5)  = 2

So the trapezoid has a height of  5 + 2 =  7

And the bases are 10 and 4

Area =   (1/2) (7) (10 + 4)  =  49

(x^2 + 1/x)  * ( x^3  + 3x^2* x^4 + 3x (x^4)^2  + (x^4)^3 )  =

(x^2 + 1/x)  * ( x^3 + 3x^6 + 3x^9 + x^12)  =

( x ^3 + 1)  / x  * ( x^3 + 3x^6 + 3x^9 + x^12)  =

(x ^3 + 1) ( x^2 + 3x^5 + 3x^8 + x^11)  = 

(x ^2 + 3x^5 + 3x^8 + x^11) +  (x^5 + 3x^8 + 3x^11 + x^14)  =

x^14 + 4x^11  + 6x^8 + 4x^5 + x^2

x^2  + 12x + y^2 + 2y =  10    complete the square on x,y

x^2 + 12x  + 36 + y^2 + 2y + 1 =  10 +36 + 1

(x + 6)^2 + ( y + 1)^2  =   47

47  = r^2

Area  = 

pi* r^2

47 pi

Here :

https://web2.0calc.com/questions/coordinates_6772