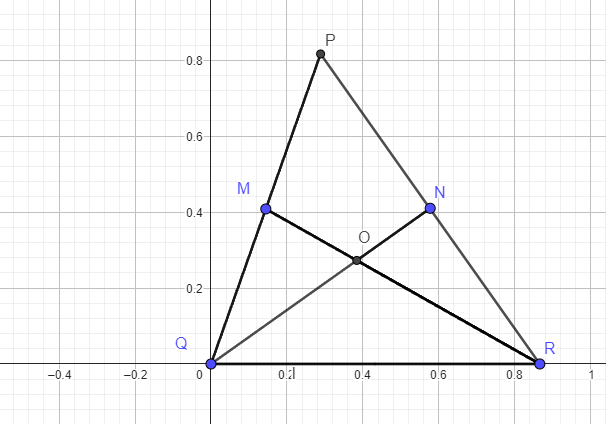
Let Q = (0,0)
QN = 1 RN = (PR/2) = 1/2 = PR
Triangle QNR is right with QNR the right angle
Then let QR = sqrt [ QR^2 - RN^2 ] = sqrt [ 1 - (1/2)^2 ] = sqrt (3/2)
So R = (sqrt (3) / 2, 0)
Also QP = sqrt [ QR^2 - PR^2 ] = sqrt [ 1 -(1/2)^2] = sqrt (3/2)
Now we can find the coordinates of P by the intersection of two circles
One centered at (0,0) wih a radius of sqrt (3)/ 2
And one centered at R = (sqrt (3) / 2 , 0) with a radius of 1
The equations are
x^2 + y^2 = 3/4 → y^2 = (3/4) - x^2
(x - sqrt (3)/2)^2 + y^2 = 1 → y^2 = 1 - (x - sqrt (3)/2)^2
Setting these equal and solving for the x coordinate of P
(3/4) - x^2 = 1 - (x - sqrt (3)/2 / 2)^2
(3/4) - x^2 = 1 - x^2 + sqrt (3)x - (3/4)
1/2 = sqrt (3) x
x = 1/ (2sqrt 3) = sqrt (3) / 6
And y^2 = (3/4) - 3 / 36 = 3/4 - 1/12 = 32/48 = 2/3
y = sqrt (2/3)
So P = ( sqrt (3) / 6 , sqrt (2/3))
Since N is a median of QP......then N = (sqrt (3) /12 , sqrt (2/3) / 2 )
O is the intersection of medians QN and RN { O is the centroid of PQR)
By a property of centroids.... ON is (2/3) the distance from R to N
(2/3) sqrt [ (sqrt (3)/2 - sqrt (3)/12)^2 + ( sqrt (2/3) /2)^2 ]
(2/3) sqrt [ (5sqrt (3)/12)^2 + ( sqrt (2/3) /2 )^2 ] =
(2/3) sqrt [ 75/144 + 1/6 ] =
(2/3) sqrt [75 /144 + 24/144 ] =
(2/3) sqrt (99 / 144) =
(2/3) (1/12) sqrt (99) =
3 (2/3) (1/12) sqrt (11) =
sqrt (11) / 6


