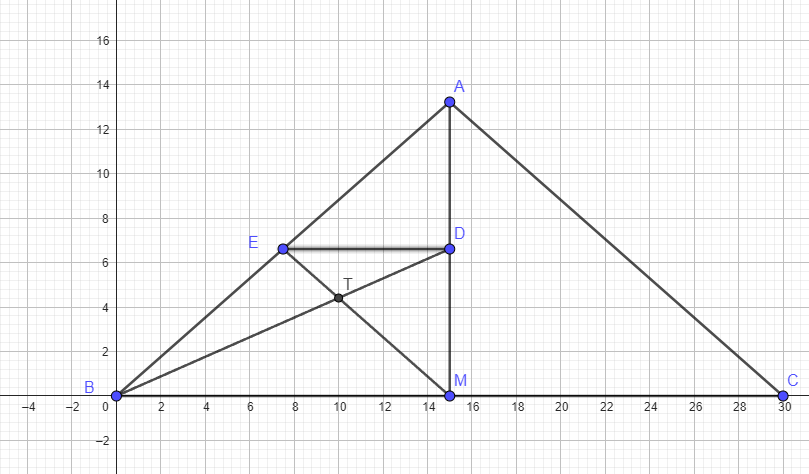
AM = sqrt [ 20^2 - 15^2] = sqrt [175 ] = 5sqrt (7)
DM = AM / 2 = 2.5 sqrt (7)
Draw ED
Triangle AED ≈ Triangle ABM
AD / AM = ED / BM
(1/2)AM / AM = ED / BM
1/2 = ED / BM
ED = (1/2) BM
Triangle EDT ≈ BMT
Since ED = 1/2 BM
Then the height of triangle EDT is 1/2 the height of triangle BMT
So the height of triangle BMT = [ 2 /( 1 + 2) ] * DM = (2/3)DM
And the height of triangle BME = DM
So the area of triangle BME = (1/2)(BM)((DM)
And the area of triangle BMT = (1/2)(BM)(2/3)(DM) = (1/3) (BM)(DM)
So the area of triangle BET = [ BME ] - [ BMT ] =
(1/2)(BM)(DM) - (1/3) (BM)(DM) = (1/6) (BM) (DM) =
(1/6) (15) ( 2.5 sqrt (7) ) =
6.25 sqrt 7 =
25sqrt (7) / 4


