heureka

Evaluate the expression. Write your answer in simplest form.
1920+(-1820)+1720+(-1620)+ ... +(-420)+320+(-220)+120=

\(\small{ \begin{array}{|rcll|} \hline && \underbrace{1920-1820}_{=100} +\underbrace{1720-1620}_{=100} +\underbrace{1520-1420}_{=100} +\underbrace{1320-1220}_{=100} +\underbrace{1120-1020}_{=100} +\underbrace{920-820}_{=100} +\underbrace{720-620}_{=100} +\underbrace{520-420}_{=100} +\underbrace{320-220}_{=100} +120 \\ &=& 9\cdot 100 + 120 \\ &=& 900 + 120 \\ &=& \mathbf{1020} \\ \hline \end{array} } \)

In triangle ABC, AB = 3, AC = 6, BC = 8, and D lies on BC such that AD bisects ∠BAC. Find cos ∠BAD.

\(\begin{array}{|rcll|} \hline \mathbf{\cos(\angle BAD)} &=& \mathbf{\sqrt{\dfrac{s\cdot (s-BC)}{AB\cdot AC} }} \quad | \quad \mathbf{s = \dfrac{AB+AC+BC}{2}}=\dfrac{3+6+8}{2}=8.5 \\\\ &=& \sqrt{\dfrac{8.5\cdot (8.5-8)}{3\cdot 6} } \\\\ &=& \sqrt{\dfrac{8.5\cdot (0.5)}{18} } \\\\ &=& \sqrt{\dfrac{4.25}{18} } \\\\ &=& \sqrt{\dfrac{2.125}{9} } \\\\ &=& \dfrac{\sqrt{ 2.125 }}{3} \\\\ &=& \dfrac{\sqrt{ 2.125 }}{3} \\\\ \mathbf{\cos(\angle BAD)} &=& \mathbf{ 0.48591265790 } \\ \hline \end{array} \)

I have to find the power series solution to this differential equation (\(y'' - 2xy' + y = 0\))
giving that \(y(0)=0\) and \(y'(0)=1\)  .

\(\begin{array}{|lcll|} \hline \text{power series}: \\ \hline y = \sum \limits_{n=0}^{\infty}a_nx^n &=& a_0 +a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5+\cdots \\\\ y' = \sum \limits_{n=1}^{\infty}na_nx^{n-1} &=& a_1 +2a_2x+3a_3x^2+4a_4x^3+5a_5x^4+\cdots \\\\ y'' = \sum \limits_{n=2}^{\infty}n(n-1)a_nx^{n-2} &=& 2\cdot 1 \cdot a_2+3\cdot 2 \cdot a_3x+4\cdot 3 \cdot a_4x^2+5\cdot 4 \cdot a_5x^3+\cdots \\ \hline && \begin{array}{|rcll|} \hline y(0) = 0 &=& a_0 +a_1\cdot 0+a_20^2+a_30^3+a_40^4+a_50^5+\cdots \\ 0 &=& a_0 \\ \mathbf{a_0} &=& \mathbf{0} \\ \hline y'(0) = 1 &=& a_1 +2a_2\cdot 0+3a_30^2+4a_40^3+5a_50^4+\cdots \\ 1 &=& a_1 \\ \mathbf{a_1} &=& \mathbf{1} \\ \hline \end{array} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline y'' - 2xy' + y &=& 0 \\ \sum \limits_{n=2}^{\infty}n(n-1)a_nx^{n-2} - 2x\sum \limits_{n=1}^{\infty}na_nx^{n-1} + \sum \limits_{n=0}^{\infty}a_nx^n &=& 0 \\ \cdots \\ \mathbf{\text{see: https://www.youtube.com/watch?v=SS6bniyB7rw }} \\ \cdots \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline y &=& a_0 \left( 1-\dfrac{1}{2!}x^2 - \sum \limits_{n=2}^{\infty} \dfrac{3\cdot 7 \cdot 11\cdots(4n-5)} {(2n)!} x^{2n} \right) +a_1 \left( x+\sum \limits_{n=1}^{\infty} \dfrac{1\cdot 5 \cdot 9 \cdots(4n-3)} {(2n+1)!} x^{2n+1} \right) \\ \hline \mathbf{a_0} &=& \mathbf{0} \\ \mathbf{a_1} &=& \mathbf{1} \\ \mathbf{y} &=& \mathbf{ x+\sum \limits_{n=1}^{\infty} \dfrac{1\cdot 5 \cdot 9 \cdots(4n-3)} {(2n+1)!} x^{2n+1} } \\ \hline \end{array}\)

There exist real numbers A and B so that \(\mathbf{ \dfrac{1}{k(k+3)} } = \mathbf{ \dfrac{A}{k} + \dfrac{B}{k+3} }\)
for all real numbers k other than 0 and -3. Find the ordered pair (A,B)

\(\begin{array}{|lrcll|} \hline &\mathbf{ \dfrac{1}{k(k+3)} } &=& \mathbf{ \dfrac{A}{k} + \dfrac{B}{k+3} } \\\\ &&& \boxed{k \neq 0 \text{ and } k \neq -3 } \\\\ &\dfrac{1}{k(k+3)} &=& \dfrac{A}{k} + \dfrac{B}{k+3} \quad | \quad \cdot k(k+3) \\\\ &\dfrac{k(k+3)}{k(k+3)} &=& \dfrac{Ak(k+3)}{k} + \dfrac{Bk(k+3)}{k+3} \\\\ &\mathbf{ 1 } &=& \mathbf{ A (k+3) + Bk } \\ \hline k=0: & 1 &=& A (0+3) + B\cdot 0 \\ & 1 &=& 3A \\ & \mathbf{A} &=& \mathbf{ \dfrac{1}{3} } \\ \hline k=-3: & 1 &=& A (-3+3) + B\cdot (-3) \\ & 1 &=& A \cdot 0 -3B \\ & 1 &=& -3B \\ & \mathbf{B} &=& \mathbf{ -\dfrac{1}{3} } \\ \hline \end{array} \)

Triangle \(ABC\) is acute. Point \(D\) lies on \(\overline {AC}\) so that \(\overline {BD}\perp \overline {AC}\),
and point \(E\) lies on \(\overline {AB}\) such that \(\overline {CE}\perp\overline {AB}\).
The intersection of segments \(\overline {CE}\) and \(\overline {BD}\)is \(P\).
Find the value of \(\overline{AE}\)  if \(CP=10\), \(PE=20\), and \(EB=30\).

\(\begin{array}{|rcll|} \hline \tan(\alpha) = \dfrac{x}{20} &=& \dfrac{10+20}{30} \\\\ \dfrac{x}{20} &=& 1 \\\\ x &=& 20 \\\\ \mathbf{\overline{AE}} &=& \mathbf{20} \\ \hline \end{array}\)

Questions 2:

1.
The greatest integer function, \(\lfloor x\rfloor\)r, denotes the largest integer less than or equal to \(x\). For example, \(\lfloor3.5\rfloor=3\), and \(\lfloor -\pi\rfloor=-4\).

Find the sum of the three smallest positive solutions to \(x-\lfloor x\rfloor=\frac1{\lfloor x\rfloor}\).
Express your answer as a mixed number.

\(\text{Let $ \text{frac}(x) = x - \lfloor x\rfloor $ } \\ \text{Let $ x = \lfloor x\rfloor + \text{frac}(x) $ } \)

I assume:

\(\begin{array}{|rcll|} \hline x-\lfloor x\rfloor &=& \frac1{\lfloor x\rfloor} \quad | \quad x - \lfloor x\rfloor = \text{frac}(x) \\ \text{frac}(x) &=& \frac1{\lfloor x\rfloor} \\ \mathbf{\lfloor x\rfloor \cdot \text{frac}(x)} &=& \mathbf{1} \\ \hline \end{array} \)

\(\begin{array}{|rclcl|c|} \hline \mathbf{\lfloor x\rfloor } &\cdot& \mathbf{\text{frac}(x)} &=& \mathbf{1}& x = \lfloor x\rfloor + \text{frac}(x) \\ \hline 2 &\cdot& \dfrac{1}{2} &=& 1 & 2\dfrac{1}{2} \\ \hline 3 &\cdot& \dfrac{1}{3} &=& 1 & 3\dfrac{1}{3} \\ \hline 4 &\cdot& \dfrac{1}{4} &=& 1 & 4\dfrac{1}{4} \\ \hline 5 &\cdot& \dfrac{1}{5} &=& 1 & 5\dfrac{1}{5} \\ \hline 6 &\cdot& \dfrac{1}{6} &=& 1 & 6\dfrac{1}{6} \\ \hline &\ldots &&&&\ldots \\ \hline \end{array} \)

The sum of the three smallest positive solutions is \(2\dfrac{1}{2}+3\dfrac{1}{3}+4\dfrac{1}{4} = 10\dfrac{1}{12} = 10.08\overline{3}\)

Thank you, CPhill !

For a triangle XYZ, we use [XYZ] to denote its area.
Let ABCD be a square with side length 1.
Points E and F lie on line BC and line CD, respectively, in such a way that angle EAF=45 degrees
If [CEF]=1/9, what is the value of [AEF].

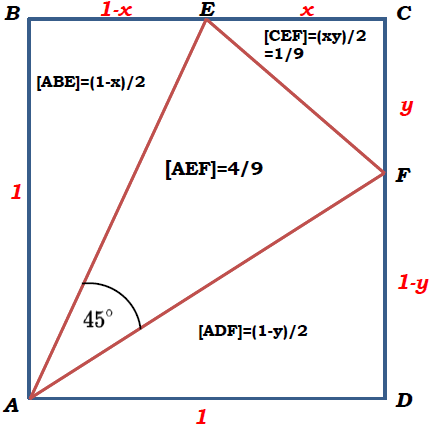
\(\text{Let $CE=x$ } \\ \text{Let $BE=1-x$ } \\ \text{Let $CF=y$ } \\ \text{Let $DF=1-y$ } \\ \text{Let $AB=AD=1$ }\)

\(\begin{array}{|lrcll|} \hline & [CEF] = \dfrac{xy}{2} &=& \dfrac{1}{9} \\\\ \text{or}& xy &=& \dfrac{2}{9} \\\\ \text{or}& y &=& \dfrac{2}{9x} \\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline &[AEF] &=& [ABCD] - [CEF]-[ABE]-[ADF] \\\\ &[AEF] &=& 1 - \dfrac{xy}{2}-\dfrac{(1-x)}{2}-\dfrac{(1-y)}{2} \quad | \quad \cdot 2 \\\\ &2[AEF] &=& 2 - xy- (1-x)-(1-y) \\ &2[AEF] &=& 2 - xy- 1+x-1+y \\ (1) &\mathbf{2[AEF]} &=& \mathbf{(x+y) - xy} \\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline &2[AEF] &=& AE\cdot AF\cdot \sin(45^\circ) \quad | \quad AE=\sqrt{1^2+(1-x)^2},\ AF=\sqrt{1^2+(1-y)^2} \\\\ &2[AEF] &=& \sqrt{1^2+(1-x)^2}\sqrt{1^2+(1-y)^2} \sin(45^\circ) \quad | \quad \sin(45^\circ) = \dfrac{\sqrt{2}} {2} \\\\ (2) &\mathbf{2[AEF]} &=& \mathbf{\sqrt{1^2+(1-x)^2}\sqrt{1^2+(1-y)^2}\cdot \dfrac{\sqrt{2}} {2} } \\ \hline \end{array}\)

(1) = (2):

\(\small{ \begin{array}{|rcll|} \hline \mathbf{(x+y) - xy} &=& \mathbf{\sqrt{1^2+(1-x)^2}\sqrt{1^2+(1-y)^2}\cdot \dfrac{\sqrt{2}} {2} } \quad | \quad \text{square both sides} \\\\ \Big((x+y) - xy\Big)^2 &=& \left(\sqrt{1^2+(1-x)^2}\sqrt{1^2+(1-y)^2}\cdot \dfrac{\sqrt{2}} {2} \right)^2 \\\\ \Big((x+y) - xy\Big)^2 &=& \left(1^2+(1-x)^2 \right) \left(1^2+(1-y)^2 \right)\cdot \dfrac{1} {2} \\\\ 2\Big((x+y) - xy\Big)^2 &=& \left(1^2+(1-x)^2 \right) \left(1^2+(1-y)^2 \right) \\ 2\Big( (x+y)^2-2(x+y)xy+x^2y^2 \Big) &=& 1+(1-y)^2+(1-x)^2+(1-x)^2(1-y)^2 \\ 2\Big( x^2+y^2 +2xy-2(x+y)xy+x^2y^2 \Big) &=& 1+1-2y+y^2+1-2x+x^2+(1-2x+x^2)(1-2y+y^2) \\ 2x^2+2y^2 +4xy-4(x+y)xy+2x^2y^2 &=& 3-2y+y^2-2x+x^2+1-2y+y^2 -2x+4xy-2xyy +x^2-2xyx+x^2y^2 \\ -4(x+y)xy+2x^2y^2 &=& 4-2y -2x -2y -2x -2xyy -2xyx+x^2y^2 \\ -4(x+y)xy+2x^2y^2 &=& 4-4(x+y) -2xy(x+y)+x^2y^2 \\ 4(x+y)-4xy(x+y)+2xy(x+y)+x^2y^2-4&=& 0 \\ (x+y)(4-4xy+2xy)+x^2y^2-4 &=& 0 \\ (x+y)(4-2xy)+x^2y^2-4 &=& 0 \quad | \quad y = \dfrac{2}{9x} \\ (x+\dfrac{2}{9x})(4-2xy)+x^2y^2-4 &=& 0 \\ \left(\dfrac{9x^2+2}{9x}\right)(4-2xy)+x^2y^2-4 &=& 0 \quad | \quad \cdot 9x \\\\ (9x^2+2)(4-2xy)+ 9x(x^2y^2-4) &=& 0 \quad | \quad \cdot 9x \\ 9x^2(4-2xy)+9x(x^2y^2-4)+2(4-2xy)&=& 0 \quad | \quad xy = \dfrac{2}{9} \\ 9x^2(4-\dfrac{4}{9})+9x(\dfrac{4}{81}-4)+2(4-\dfrac{4}{9})&=& 0 \\ 9x^2(\dfrac{36-4}{9})+9x(\dfrac{-320}{81})+2(\dfrac{36-4}{9})&=& 0 \\ 9x^2(\dfrac{32}{9})-x(\dfrac{-320}{9})+2(\dfrac{32}{9})&=& 0 \\ 32x^2-\dfrac{320}{9}x+ \dfrac{64}{9} &=& 0 \quad | \quad \cdot 9 \\ 288x^2-320x+64&=& 0 \quad | \quad :4 \\ \mathbf{ 72x^2-80x+16 } &=& \mathbf{0} \\ \hline \end{array} }\)

\(\begin{array}{|lrcll|} \hline & \mathbf{ 72x^2-80x+16 } &=& \mathbf{0} \\ & x &=& \dfrac{5}{9} + \dfrac{\sqrt{7}}{9} \\ \text{or}& x &=& \dfrac{5}{9} - \dfrac{\sqrt{7}}{9} \\\\ & y &=& \dfrac{5}{9} - \dfrac{\sqrt{7}}{9} \\ \text{or}& y &=& \dfrac{5}{9} + \dfrac{\sqrt{7}}{9} \\\\ & 2[AEF] &=& (x+y) -xy \\ & 2[AEF] &=& \left(\dfrac{5}{9} + \dfrac{\sqrt{7}}{9}+\dfrac{5}{9} - \dfrac{\sqrt{7}}{9} \right) - \left(\dfrac{5}{9} + \dfrac{\sqrt{7}}{9}\right) \left(\dfrac{5}{9} - \dfrac{\sqrt{7}}{9}\right) \\ & 2[AEF] &=& \dfrac{10}{9} - \left(\dfrac{5^2}{9^2} - \dfrac{(\sqrt{7})^2}{9^2}\right) \\ & 2[AEF] &=& \dfrac{10}{9} - \dfrac{2}{9} \\ & 2[AEF] &=& \dfrac{8}{9} \\ & \mathbf{ [AEF] } &=& \mathbf{ \dfrac{4}{9} } \\ \hline \end{array}\)

What is the value of \(\sum \limits_{n=1}^\infty \left(\tan^{-1}(\sqrt{n})-\tan^{-1}(\sqrt{n+1})\right)\)?

\(I\ assume \ \boxed{\tan^{-1}(x) = \arctan(x)} \)

\(\begin{array}{|rcll|} \hline && \sum \limits_{n=1}^\infty \left(\arctan(\sqrt{n})-\arctan(\sqrt{n+1})\right) \\\\ &=& \overbrace{ \arctan(\sqrt{1})-\arctan(\sqrt{2}) }^{n=1} \\ && + \quad\qquad \qquad \quad \overbrace{ \arctan(\sqrt{2})-\arctan(\sqrt{3}) }^{n=2} \\ && + \qquad\qquad \qquad \qquad \qquad \quad\quad \overbrace{ \arctan(\sqrt{3})-\arctan(\sqrt{4}) }^{n=3} \\ && \cdots \\ && + \overbrace{ \arctan(\sqrt{\infty})-\arctan(\sqrt{\infty+1}) }^{n=\infty} \\ \hline \end{array} \)

\(\text{shorten} \ldots \)

\(\begin{array}{|rcll|} \hline && -\arctan(\sqrt{2})+\arctan(\sqrt{2}) \\ && -\arctan(\sqrt{3})+\arctan(\sqrt{3}) \\ && -\arctan(\sqrt{4})+\arctan(\sqrt{4}) \\ && \cdots \\ && -\arctan(\sqrt{\infty}) + \arctan(\sqrt{\infty}) \\ &=& 0 \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline && \mathbf{\sum \limits_{n=1}^\infty \left(\arctan(\sqrt{n})-\arctan(\sqrt{n+1})\right)} \\\\ &=& \arctan(\sqrt{1})-\arctan(\sqrt{\infty+1}) \\ &=& \arctan(1)-\arctan( \infty ) \\\\ &=& \dfrac{\pi}{4} - \dfrac{\pi}{2} \\\\ &=& -\dfrac{\pi}{4} \\\\ &=& \mathbf{-0.7853981634} \\ \hline \end{array}\)