heureka

Mathematical equivalents

Was ist die 101. Ableitung von \(f(x)=\cos(x)\)?

\(\begin{array}{|rcll|} \hline f(x) &=& \cos(x) \\ &=& \cos\left(0\cdot \dfrac{\pi}{2} + x \right) \\ \hline f'(x) &=& -\sin(x) \\ &=& \sin(-x) \\ &=& \cos\left(\dfrac{\pi}{2}-(-x)\right) \\ &=& \cos\left(\dfrac{\pi}{2}+x\right) \\ &=& \cos\left(1\cdot \dfrac{\pi}{2}+x\right) \\ \hline f''(x) &=& -\sin\left(1\cdot \dfrac{\pi}{2}+x\right) \\ &=& \sin\left(-(\dfrac{\pi}{2}+x) \right) \\ &=& \cos\left(\dfrac{\pi}{2}-(-(\dfrac{\pi}{2}+x)) \right) \\ &=& \cos\left(\dfrac{\pi}{2}+\dfrac{\pi}{2}+x \right) \\ &=& \cos\left(2\cdot \dfrac{\pi}{2}+x \right) \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline f(x) &=& \cos\left(0\cdot \dfrac{\pi}{2} + x \right) \\ f'(x) &=& \cos\left(1\cdot \dfrac{\pi}{2}+x\right) \\ f''(x) &=& \cos\left(2\cdot \dfrac{\pi}{2}+x \right) \\ \cdots \\ \mathbf{f^n(x)} &=& \mathbf{\cos\left(n\cdot \dfrac{\pi}{2}+x\right)} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{f^n(x)} &=& \mathbf{\cos\left(n\cdot \dfrac{\pi}{2}+x\right)} \\\\ f^{101}(x) &=& \cos\left(101\cdot \dfrac{\pi}{2}+x\right) \quad & | \quad 101\cdot \dfrac{\pi}{2} = 25\cdot (2\pi) + \dfrac{\pi}{2} \\ &=& \cos\left(25\cdot (2\pi) + \dfrac{\pi}{2}+x\right) \\ &=& \cos\left(\dfrac{\pi}{2}+x\right) \\ \mathbf{f^{101}(x)} &=& \mathbf{-\sin\left(x\right) } \\ \hline \end{array}\)

Thank you, CPhill !

What is the sum of the following sequence:

\(1^{-6} + 3^{-6} + 5^{-6} + 7^{-6} + 9^{-6} + \ldots\) to infinity.

\(\begin{array}{|rcll|} \hline 1^{-6} + 3^{-6} + 5^{-6} + 7^{-6} + 9^{-6} + \ldots &=& 1+\dfrac{1}{3^6}+\dfrac{1}{5^6}+\dfrac{1}{7^6}+\dfrac{1}{9^6}+ \ldots \\ &=& \sum \limits_{n=0}^{\infty} \dfrac{1}{(2n+1)^6} \\ \hline \end{array}\)

zeta-function:

\(\begin{array}{|rcll|} \hline \zeta(s) &=& 1+\dfrac{1}{2^s}+\dfrac{1}{3^s}+\dfrac{1}{4^s}+\dfrac{1}{5^s}+ \ldots \\ \zeta(s)\left(1-\dfrac{1}{2^s} \right) &=& \left( 1+\dfrac{1}{2^s}+\dfrac{1}{3^s}+\dfrac{1}{4^s}+\dfrac{1}{5^s}+ \ldots \right) \left(1-\dfrac{1}{2^s} \right) \\ &=& \left( 1+\dfrac{1}{2^s}+\dfrac{1}{3^s}+\dfrac{1}{4^s}+\dfrac{1}{5^s}+ \ldots \right) \\ && -\left(\dfrac{1}{2^s}+\dfrac{1}{4^s}+\dfrac{1}{6^s}+\dfrac{1}{8^s} \right) \\ \mathbf{\zeta(s)\left(1-\dfrac{1}{2^s} \right) } &=& \mathbf{ 1+\dfrac{1}{3^6}+\dfrac{1}{5^6}+\dfrac{1}{7^6}+\dfrac{1}{9^6}+ \ldots } \\ \hline \end{array} \)

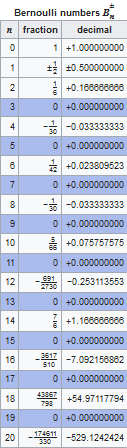
with Bernoulli numbers B:

\(\begin{array}{|lrcll|} \hline & \sum \limits_{n=0}^{\infty} \dfrac{1}{(2n+1)^s} &=& \left(1-\dfrac{1}{2^s} \right) \zeta(s) \quad &| \quad \zeta(2n) = \Big(-1\Big)^{(n-1)} \cdot \dfrac{ (2 \pi)^{2n} } {2(2n)!} B_{2n} \\ \hline s=6: & \sum \limits_{n=0}^{\infty} \dfrac{1}{(2n+1)^6} &=& \left(1-\dfrac{1}{2^6} \right) \zeta(6) \quad &| \quad \zeta(2\cdot 3) = \Big(-1\Big)^{(3-1)} \cdot \dfrac{ (2 \pi)^{2\cdot 3} } {2(2\cdot 3)!} B_{2\cdot 3} \\ & & & \quad &| \quad \zeta(6) = \Big(-1\Big)^{2} \cdot \dfrac{ (2 \pi)^{6} } {2(6)!} B_{6} \\ & & & \quad &| \quad \zeta(6) = \dfrac{ 2^6 \pi^6 } { 2\cdot 720} B_{6} \qquad B_6 = \dfrac{1}{42} \\ & & & \quad &| \quad \zeta(6) = \dfrac{ 2^6 \pi^6 } { 2\cdot 720} \cdot \dfrac{1}{42} \\ & & & \quad &| \quad \boxed{\zeta(6) = \dfrac{ \pi^6 } {945} } \\ & \sum \limits_{n=0}^{\infty} \dfrac{1}{(2n+1)^6} &=& \left(1-\dfrac{1}{2^6} \right) \dfrac{ \pi^6 } {945} \\ & \mathbf{ \sum \limits_{n=0}^{\infty} \dfrac{1}{(2n+1)^6} } &=& \mathbf{ \dfrac{ \pi^6 } {960 } } \\ \hline \end{array}\)

Bernoulli numbers:

Factor the expression given below.
Write each factor as a polynomial in descending order.
\(100w^2 x^2 - 36y^2 z^2\)

\(\begin{array}{|rcll|} \hline && 100w^2 x^2 - 36y^2 z^2 \\ &=& \left(10w x - 6y z\right) \left(10w x + 6y z\right) \\ \hline \end{array}\)

The graph above is the graph of \(y=x^2\) translated and reflected in the xy-plane.
Find an equation for this graph.

1. translated

\(\begin{array}{|rcll|} \hline y_0 &=& x_0^2 \\ && \boxed{y = y_0+2\\ x=x_0+7 } \\ (y-2) &=& (x-7)^2 \\ y &=& 2 + (x-7)^2 \quad \text{ after translation} \\ \hline \end{array}\)

2. reflected

\(\begin{array}{|rcll|} \hline y_0 &=& 2 + (x_0-7)^2 \\ && \boxed{y = -y_0\\ x=x_0 } \\ -y &=& 2+(x-7)^2 \\ \mathbf{y} &=& \mathbf{-2-(x-7)^2} \quad \text{ after translation and reflextion} \\ \hline \end{array}\)

Define #N by the formula #N = 0.5(N) + 1.
Calculate #(#(#50)).

\(\begin{array}{|rcll|} \hline \mathbf{\#N} &=& \mathbf{\dfrac{N}{2} + 1} \\\\ \#50 &=& \dfrac{50}{2} + 1 \\ &=& 26 \\\\ \#26 &=& \dfrac{26}{2} + 1 \\ &=& 14 \\\\ \#14 &=& \dfrac{14}{2} + 1 \\ &=& 8 \\\\ \mathbf{ \#(\#(\#50)) } &=& \mathbf{8} \\ \hline \end{array}\)

Thank you, JoshuaGreen !

​ Please help

\(\dfrac{\sec^2 \left(\dfrac{4}{x} \right)-1}{\cos \left(\dfrac{6}{x} \right)-\cos \left(\dfrac{2}{x} \right)} \)

\(\begin{array}{|rcll|} \hline && \mathbf{\dfrac{\sec^2 \left(\dfrac{4}{x} \right)-1}{\cos \left(\dfrac{6}{x} \right)-\cos \left(\dfrac{2}{x} \right)}} \\\\ &&\qquad \boxed{\sec^2 \left(\dfrac{4}{x} \right)-1 = \dfrac{\sin^2 \left(\dfrac{4}{x} \right)}{\cos^2 \left(\dfrac{4}{x} \right)} \\~\\= \sin^2 \left(\dfrac{4}{x} \right)\sec^2 \left(\dfrac{4}{x} \right) } \\\\ &=& \dfrac{\sin^2 \left(\dfrac{4}{x} \right)\sec^2 \left(\dfrac{4}{x} \right) } {\cos \left(\dfrac{6}{x} \right)-\cos \left(\dfrac{2}{x} \right)} \\\\ &&\qquad \boxed{ \cos \left(\dfrac{6}{x} \right)-\cos \left(\dfrac{2}{x} \right) = -2\sin \left( \dfrac{6+2}{x} \above 1pt 2 \right) \sin \left( \dfrac{6-2}{x}\above 1pt 2 \right) \\~\\= -2\sin \left(\dfrac{4}{x} \right) \sin \left(\dfrac{2}{x} \right) } \\\\ &=& \dfrac{\sin^2 \left(\dfrac{4}{x} \right)\sec^2 \left(\dfrac{4}{x} \right) } {-2\sin \left(\dfrac{4}{x} \right) \sin \left(\dfrac{2}{x} \right)} \\\\ &=& -\dfrac{\sin \left(\dfrac{4}{x} \right)\sec^2 \left(\dfrac{4}{x} \right) } {2 \sin \left(\dfrac{2}{x} \right)} \\\\ &=& -\dfrac{\sin \left(2\cdot \dfrac{2}{x} \right)\sec^2 \left(\dfrac{4}{x} \right) } {2 \sin \left(\dfrac{2}{x} \right)} \\\\ &&\qquad \boxed{ \sin \left(2\cdot \dfrac{2}{x} \right) = 2 \sin \left(\dfrac{2}{x} \right)\cos \left(\dfrac{2}{x} \right) } \\\\ &=& -\dfrac{ 2 \sin \left(\dfrac{2}{x} \right)\cos \left(\dfrac{2}{x} \right)\sec^2 \left(\dfrac{4}{x} \right) } {2 \sin \left(\dfrac{2}{x} \right)} \\\\ &=& \mathbf{-\cos \left(\dfrac{2}{x} \right)\sec^2 \left(\dfrac{4}{x} \right)} \\ \hline \end{array}\)

If a*b=2a+3b for all a and b, then what is the value of 4*3

\(\begin{array}{|rcll|} \hline 4*3 &=& 2\cdot 4 + 3\cdot 3 \\ &=& 8+9 \\ &=& \mathbf{17} \\ \hline \end{array}\)