heureka

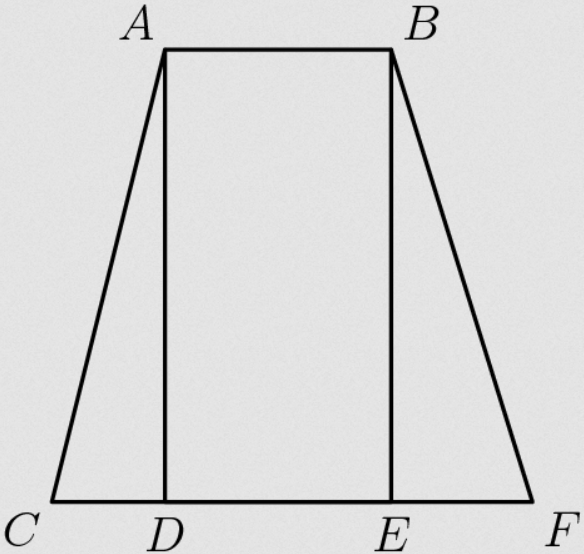
The area of trapezoids ABEC, ABFD, and ABFC are 133, 140, and 161 square feet, respectively.

Quadrilateral ABED is a rectangle.

The length of segment DE is 8 feet.

What is the length of segment CF?

\(\text{Let $A_1= ABEC = 133$} \\ \text{Let $A_2= ABFD = 140$} \\ \text{Let $A = ABFC = 161$} \\ \text{Let $A_{\text{rectangle}}=A_\square = 8 AD $} \\ \text{Let $x = CF$} \)

\(\begin{array}{|rcll|} \hline A_1 + A_2 &=& A + A_\square \\ 133+140 &=& 161 + A_\square \\ A_\square &=& 133+140- 161 \\ \mathbf{A_\square} &=& \mathbf{112} \quad | \quad A_\square = 8 AD \\ 8 AD &=& 112 \\ AD &=& \dfrac{112}{8} \\ \mathbf{AD} &=& \mathbf{14} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline A &=& \dfrac{(8+x)}{2}*AD \\ 161 &=& \dfrac{(8+x)}{2}*14 \\ 161 &=& (8+x)*7 \\ 23 &=& 8+x \\ x &=& 23-8 \\ \mathbf{x} &=& \mathbf{15} \\ \hline \end{array}\)

The length of segment CF is 15

If
\(\sin(x) + \cos(x) = \dfrac{1}{2}\),
find
\(\sin^3(x) + \cos^3(x)\).

\(\begin{array}{|rcll|} \hline \Big( \sin(x) + \cos(x) \Big)^2 &=& \sin^2(x) + 2\sin(x)\cos(x)+\cos^2(x) \\ \Big( \sin(x) + \cos(x) \Big)^2 &=& \sin^2(x)+\cos^2(x) + 2\sin(x)\cos(x) \quad | \quad \sin^2(x)+\cos^2(x)=1 \\ \Big( \sin(x) + \cos(x) \Big)^2 &=& 1 + 2\sin(x)\cos(x) \quad | \quad \sin(x) + \cos(x) = \dfrac{1}{2} \\ \Big(\dfrac{1}{2} \Big)^2 &=& 1 + 2\sin(x)\cos(x) \\ 2\sin(x)\cos(x) &=& \dfrac{1}{4} - 1 \\ 2\sin(x)\cos(x) &=& -\dfrac{3}{4} \\ \mathbf{ \sin(x)\cos(x) } &=& \mathbf{-\dfrac{3}{8} } \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \Big(\sin^2(x) + \cos^2(x)\Big)\Big( \sin(x) + \cos(x) \Big) &=& \sin^3(x) +\sin^2(x)\cos(x) +\cos^2(x)\sin(x) + \cos^3(x) \\ \Big(\sin^2(x) + \cos^2(x)\Big)\Big( \sin(x) + \cos(x) \Big) &=& \sin^3(x)+\cos^3(x) +\sin(x)\cos(x)\Big(\sin(x) +\cos(x)\Big) \\ 1*\dfrac{1}{2} &=& \sin^3(x)+\cos^3(x) -\dfrac{3}{8}*\dfrac{1}{2} \\ \dfrac{1}{2} &=& \sin^3(x)+\cos^3(x) -\dfrac{3}{16} \\ \sin^3(x)+\cos^3(x) &=& \dfrac{3}{16}+\dfrac{1}{2} \\ \mathbf{ \sin^3(x)+\cos^3(x) } &=& \mathbf{ \dfrac{11}{16} } \\ \hline \end{array}\)

Find the number of equilateral triangles in the grid (\(n=5\)).

\(a(n) = \Big\lfloor \dfrac{n(n+2)(2n+1)}{8} \Big \rfloor \)

Farmer Jim has an 8 gallon bucket full with water. He has three empty buckets: 3 gallons, 5 gallons and 8 gallons.

How can he get two volumes of water, 4 gallons each, using only the four buckets?

\(\begin{array}{|l|c|c|c|c|} \hline \text{buckets } & 8\ \text{gallons }& 3\ \text{gallons }& 5\ \text{gallons }& 8\ \text{gallons } \\ \hline \text{Start} & 8 & 0& 0& 0 \\ & 5 & 3& 0& 0 \\ & 5 & 0& 3& 0 \\ & 2 & 3& 3& 0 \\ & 2 & 1& 5& 0 \\ & 2 & 0& 5& 1 \\ & 2 & 3& 2& 1 \\ & 4 & 3& 0& 1 \\ \text{End} & 4 & 0& 0& 4 \\ \hline \end{array}\)

Let \(m > 1\) be a positive integer. 

Find the remainder when \(2^m + 5^{m - 1} + 7^{m - 2}\) is divided by 3.

\(\begin{array}{|rcll|} \hline && 2^m + 5^{m - 1} + 7^{m - 2} \\ &\equiv& (3-1)^m + (6-1)^{m - 1} + (6+1)^{m - 2} \\ &\equiv& \binom{m}{0}3^{m} - \binom{m}{1}3^{m-1}+ \binom{m}{2}3^{m-2}+-\ldots \pm \binom{m}{m} \\ && +\binom{m-1}{0}6^{m-1} - \binom{m-1}{1}6^{m-2}+ \binom{m-1}{2}6^{m-3}+-\ldots \mp \binom{m-1}{m-1} \\ && +\binom{m-2}{0}6^{m-2} \binom{m-2}{1}6^{m-3}+ \binom{m-2}{2}6^{m-4}+\ldots + \binom{m-2}{m-2} \\ &\equiv& \underbrace{\pm \binom{m}{m} \mp \binom{m-1}{m-1}}_{=0}+ \underbrace{\binom{m-2}{m-2}}_{=1} \\ &\equiv& \mathbf{1} \pmod{ 3 } \\ \hline \end{array}\)

If
\(\dfrac{a + b}{a} = \dfrac{a}{b} = x\), and \(x\) is positive, then find \(x\).

\(\begin{array}{|rcll|} \hline \dfrac{a + b}{a} &=& \dfrac{a}{b} \\\\ \dfrac{a}{a}+\dfrac{b}{a} &=& \dfrac{a}{b} \\\\ 1+\dfrac{b}{a} &=& \dfrac{a}{b} \quad | \quad \dfrac{a}{b} = x,\ \dfrac{b}{a} = \dfrac{1}{x} \\\\ 1+\dfrac{1}{x} &=& x \quad | \quad \times x \\\\ x+ 1 &=& x^2 \\ x^2-x-1 &=& 0 \\\\ x &=& \dfrac{1\pm \sqrt{1-4(-1)}} {2} \\ x &=& \dfrac{1\pm \sqrt{5}} {2} \quad | \quad x\ \text{is positive} \\ \mathbf{x} &=& \mathbf{\dfrac{1 + \sqrt{5}} {2}} \qquad (x=1.61803398875) \\ \hline \end{array}\)

The real roots of \(2x^3 - 7x^2 + kx - 2 = 0\) are in geometric progression.  
Find these three roots.

\(\begin{array}{|rcll|} \hline 2(x-a_1)(x-a_1r)(x-a_1r^2) &=& 2x^3 - 7x^2 + kx - 2 = 0 \\ \ldots \\ 2\left(x^3-a_1(r^2+r+1)x^2+a_1^2(r^3+r^2+r)x-a_1^3r^3 \right) &=& 2x^3 - 7x^2 + kx - 2 = 0 \\ 2\left(x^3-a_1(r^2+r+1)x^2+a_1^2r(r^2+r+1)x-a_1^3r^3 \right) &=& 2x^3 - 7x^2 + kx - 2 = 0 \\ 2x^3\underbrace{-2a_1(r^2+r+1)}_{=-7}x^2+\underbrace{2a_1^2r(r^2+r+1)}_{=k}x\underbrace{-2a_1^3r^3}_{=-2} &=& 2x^3 - 7x^2 + kx - 2 = 0 \\ \text{compare} \\ -2a_1^3r^3=-2 \\ a_1^3r^3= 1 \\ a_1 r = 1 \\ \mathbf{a_1=\dfrac{1}{r}} \\\\ -2a_1(r^2+r+1)=-7 \\ 2a_1(r^2+r+1)=7 \\ 2\dfrac{1}{r}(r^2+r+1)=7 \\ \mathbf{r^2+r+1=\dfrac{7r}{2}} \\\\ k = 2a_1^2r(r^2+r+1) \\ k = 2\dfrac{1}{r^2}r(r^2+r+1) \\ k = 2\dfrac{1}{r}(r^2+r+1) \\ k = 2\dfrac{1}{r}*\dfrac{7r}{2} \\ \mathbf{k = 7} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{2x^3 - 7x^2 + 7x - 2} &=& \mathbf{0} \\ x_1 &=& \dfrac{1}{2} \\ x_2 &=& 1 \\ x_3 &=& 2 \\ \text{geometric progression:}~ \dfrac{1}{2},\ \dfrac{1}{2}*2^1,\ \dfrac{1}{2}*2^2 \\ \hline \end{array} \)

Thank you, CPhill !

A sequence satisifes \(a_1 = 3\) and \(a_{n + 1} = \dfrac{a_n}{a_n + 1}\) for \(n \geq 1\). 

What is \( a_{14}\)?

\(\begin{array}{|lrcll|} \hline & \mathbf{a_{n + 1}} &=& \mathbf{\dfrac{a_n}{a_n + 1}} \\\\ & \dfrac{1}{a_{n + 1}} &=& \dfrac{a_n + 1}{a_n} \\\\ & \mathbf{\dfrac{1}{a_{n + 1}}} &=& \mathbf{1+ \dfrac{1}{a_n}} \\\\ \hline \\ & \dfrac{1}{a_{n + 2}} &=& 1+ \dfrac{1}{a_{n+1}} \quad | \quad \mathbf{\dfrac{1}{a_{n + 1}}=1+ \dfrac{1}{a_n}} \\\\ & \dfrac{1}{a_{n + 2}} &=& 1+ 1+ \dfrac{1}{a_n} \\\\ & \mathbf{\dfrac{1}{a_{n + 2}}} &=& \mathbf{2+ \dfrac{1}{a_n}} \\\\ \hline \\ & \dfrac{1}{a_{n + 3}} &=& 1+ \dfrac{1}{a_{n+2}} \quad | \quad \mathbf{\dfrac{1}{a_{n + 2}}=2+ \dfrac{1}{a_n}} \\\\ & \dfrac{1}{a_{n + 3}} &=& 1+ 2+ \dfrac{1}{a_n} \\\\ & \mathbf{\dfrac{1}{a_{n + 3}}} &=& \mathbf{3+ \dfrac{1}{a_n}} \\\\ \hline \\ & \dfrac{1}{a_{n + 4}} &=& 1+ \dfrac{1}{a_{n+3}} \quad | \quad \mathbf{\dfrac{1}{a_{n + 3}}=3+ \dfrac{1}{a_n}} \\\\ & \dfrac{1}{a_{n + 4}} &=& 1+ 3+ \dfrac{1}{a_n} \\\\ & \mathbf{\dfrac{1}{a_{n + 4}}} &=& \mathbf{4+ \dfrac{1}{a_n}} \\ \hline & \ldots \\ \hline \\ & \mathbf{\dfrac{1}{a_{n + m}}} &=& \mathbf{m+ \dfrac{1}{a_n}} \\\\ n=1,\ m=13: & \mathbf{\dfrac{1}{a_{1 + 13}}} &=& \mathbf{13+ \dfrac{1}{a_1}} \\\\ & \dfrac{1}{a_{14}} &=& 13+ \dfrac{1}{a_1} \quad | \quad a_1 =3 \\\\ & \dfrac{1}{a_{14}} &=& 13+ \dfrac{1}{3} \\\\ & \dfrac{1}{a_{14}} &=& \dfrac{3*13+1}{3} \\\\ & \dfrac{1}{a_{14}} &=& \dfrac{40}{3} \\\\ & \mathbf{ a_{14} } &=& \mathbf{\dfrac{3}{40} } \\ \hline \end{array}\)

In convex quadrialteral ABCD, the area of triangle DAB is 1, that of triangle ABC is 6, and that of triangle CDA is 2. 

Find the area of triangle BCD.

\(\begin{array}{|rcll|} \hline \mathbf{CDA + ABC} &=& \mathbf{DAB + BCD} \\ 2 + 6 &=& 1 + BCD \\ 8 &=& 1 + BCD \\ BCD &=& 8-1 \\ \mathbf{BCD} &=& \mathbf{7} \\ \hline \end{array}\)