heureka

Let \(a_0=6\) and \(a_n = \dfrac{a_{n - 1}}{1 + a_{n - 1}}\) for all \(n \ge 1\).
Find \(a_{100}\)

\(\begin{array}{|rcll|} \hline a_n &=& \dfrac{a_{n - 1}}{1 + a_{n - 1}} \\\\ \dfrac{1}{a_n} &=& \dfrac{1 + a_{n - 1}} {a_{n - 1}} \\\\ \dfrac{1}{a_n} &=& \dfrac{1} {a_{n - 1}} +\dfrac{a_{n - 1}} {a_{n - 1}} \\\\ \mathbf{\dfrac{1}{a_n}} &=& \mathbf{\dfrac{1} {a_{n - 1}} + 1} \\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline \mathbf{\dfrac{1}{a_n}} = \mathbf{\dfrac{1} {a_{n - 1}} + 1} \\ \hline n=1: & \dfrac{1}{a_1} &=& \dfrac{1} {a_{1 - 1}} + 1 \\\\ & \mathbf{\dfrac{1}{a_1}} &=& \mathbf{ \dfrac{1} {a_{0}} + 1} \\ \hline n=2: & \dfrac{1}{a_2} &=& \dfrac{1} {a_{2-1}} + 1 \\\\ & \dfrac{1}{a_2} &=& \dfrac{1} {a_{1}} + 1 \\\\ & \dfrac{1}{a_2} &=& \dfrac{1} {a_{0}} + 1 + 1 \\\\ & \mathbf{\dfrac{1}{a_2}} &=& \mathbf{\dfrac{1} {a_{0}} + 2} \\ \hline n=3: & \dfrac{1}{a_3} &=& \dfrac{1} {a_{3-1}} + 1 \\\\ & \dfrac{1}{a_3} &=& \dfrac{1} {a_{2}} + 1 \\\\ & \dfrac{1}{a_3} &=& \dfrac{1} {a_{0}} + 2 + 1 \\\\ & \mathbf{\dfrac{1}{a_3}} &=& \mathbf{\dfrac{1} {a_{0}} + 3} \\ \hline \ldots \\ \hline & \mathbf{\dfrac{1}{a_n}} &=& \mathbf{\dfrac{1} {a_{0}} + n} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\dfrac{1}{a_n}} &=& \mathbf{\dfrac{1} {a_{0}} + n} \quad | \quad a_0 = 6 \\\\ \dfrac{1}{a_n} &=& \dfrac{1} {6} + n \quad | \quad n = 100 \\\\ \dfrac{1}{a_{100}} &=& \dfrac{1} {6} + 100 \\\\ \dfrac{1}{a_{100}} &=& \dfrac{1} {6} + \dfrac{600}{6} \\\\ \dfrac{1}{a_{100}} &=& \dfrac{1+600} {6} \\\\ \dfrac{1}{a_{100}} &=& \dfrac{601} {6} \\\\ \mathbf{ a_{100} } &=& \mathbf{\dfrac{6}{601} } \\ \hline \end{array}\)

(a)
\(n\in \mathbb{N}: \qquad \sum \limits_{k=1}^{n} (k^3-1) = \left(\dfrac{n(n+1)}{2}\right)^2-n\)

\(\begin{array}{|lrcll|} \hline \mathbf{n=1}: & \sum \limits_{k=1}^{1} (k^3-1) &=& \left(\dfrac{1(1+1)}{2}\right)^2-1 \\\\ & 1^3-1 &=& \left(\dfrac{1*2}{2}\right)^2-1 \\\\ & 1 -1 &=& \left(1\right)^2-1 \\\\ & 1 -1 &=& 1-1 \ \checkmark \\ \hline \end{array}\)

\(\small{ \begin{array}{|rcll|} \hline \mathbf{n+1}: & \sum \limits_{k=1}^{n+1} (k^3-1) &=& \left(\dfrac{(n+1)\Big((n+1)+1\Big)}{2}\right)^2-(n+1) \\\\ & \sum \limits_{k=1}^{n+1} (k^3-1) &=& \left(\dfrac{(n+1)(n+2)}{2}\right)^2-(n+1) \\\\ & \sum \limits_{k=1}^{n+1} (k^3-1) &=& \dfrac{(n+1)^2(n+2)^2}{2^2} -(n+1) \\\\ & \sum \limits_{k=1}^{n+1} (k^3-1) &=& \dfrac{(n+1)^2(n+2)^2}{4} -(n+1) \\ & && \boxed{\sum \limits_{k=1}^{n+1} (k^3-1)=\sum \limits_{k=1}^{n} (k^3-1) +(n+1)^3-1 } \\ & \sum \limits_{k=1}^{n} (k^3-1) +(n+1)^3-1 &=& \dfrac{(n+1)^2(n+2)^2}{4} -(n+1) \\ & && \boxed{\text{Induktionsannahme:}\\ \sum \limits_{k=1}^{n} (k^3-1) = \left(\dfrac{n(n+1)}{2}\right)^2-n} \\ & \left(\dfrac{n(n+1)}{2}\right)^2-n +(n+1)^3-1 &=& \dfrac{(n+1)^2(n+2)^2}{4} -(n+1) \\ & \left(\dfrac{n(n+1)}{2}\right)^2 +(n+1)^3-n-1 &=& \dfrac{(n+1)^2(n+2)^2}{4} -(n+1) \\ & \left(\dfrac{n(n+1)}{2}\right)^2 +(n+1)^3-(n+1) &=& \dfrac{(n+1)^2(n+2)^2}{4} -(n+1) \\ & \dfrac{n^2(n+1)^2}{2^2} +(n+1)^3-(n+1) &=& \dfrac{(n+1)^2(n+2)^2}{4} -(n+1) \\ & \dfrac{n^2(n+1)^2}{4} +(n+1)^2(n+1)-(n+1) &=& \dfrac{(n+1)^2(n+2)^2}{4} -(n+1) \\ & (n+1)^2\left( \dfrac{n^2}{4}+(n+1)\right)-(n+1) &=& \dfrac{(n+1)^2(n+2)^2}{4} -(n+1) \\ & (n+1)^2\left( \dfrac{n^2+4(n+1)}{4}\right)-(n+1) &=& \dfrac{(n+1)^2(n+2)^2}{4} -(n+1) \\ & (n+1)^2\left( \dfrac{n^2+4n+4}{4}\right)-(n+1) &=& \dfrac{(n+1)^2(n+2)^2}{4} -(n+1) \\ & && \boxed{n^2+4n+4 = (n+2)^2 } \\ \\ & \dfrac{(n+1)^2(n+2)^2}{4}-(n+1) &=& \dfrac{(n+1)^2(n+2)^2}{4} -(n+1)\ \checkmark \\ \hline \end{array} }\)

In the diagram, BD = 5, CE = 4, [ABC] = 24, and [ADE] = 18.

Find [ACD].

\(\begin{array}{|lrcll|} \hline (1) & 24 + [ACD] &=& \dfrac{5h}{2} \\\\ (2) & 18 + [ACD] &=& \dfrac{4h}{2} \\ \hline (1)-(2): & 24 + [ACD] -(18 + [ACD]) &=& \dfrac{5h}{2}-\dfrac{4h}{2} \\\\ & 24 + [ACD] -18 - [ACD] &=& \dfrac{1h}{2} \\\\ & 24 -18 &=& \dfrac{h}{2} \\\\ & 6 &=& \dfrac{h}{2} \\\\ & \mathbf{h} &=& \mathbf{12} \\ \hline & 18 + [ACD] &=& \dfrac{4h}{2} \\ & 18 + [ACD] &=& 2h \quad & | \quad h=12 \\ & 18 + [ACD] &=& 2h \\ & 18 + [ACD] &=& 2*12 \\ & 18 + [ACD] &=& 24 \\ & [ACD] &=& 24-18 \\ & \mathbf{[ACD]} &=& \mathbf{6} \\ \hline \end{array}\)

Let  r1, r2, r3 and r4 be the roots of x^4 - 2x^3 - 5x^2 + 4x - 1 = 0
Find the monic polynomial , in x,  whose roots are 1/r1, 1/r2, 1/r3 and 1/r4 

\(\begin{array}{|rcll|} \hline \mathbf{x^4 - 2x^3 - 5x^2 + 4x - 1} &=& \mathbf{0} \\\\ r^4 - 2r^3 - 5r^2 + 4r - 1 &=& 0 \quad & | \quad : r^4 \\ 1 - 2\dfrac{1}{r} - 5\dfrac{1}{r^2} + 4\dfrac{1}{r^3} - \dfrac{1}{r^4} &=& 0 \quad & | \quad x= \dfrac{1}{r} \\ 1 - 2x - 5x^2 + 4x^3 - x^4 &=& 0 \quad & | \quad *(-1) \\ \mathbf{x^4 -4x^3 + 5x^2+2x-1} &=& \mathbf{0} \\ \hline \end{array}\)

\(\mathbf{x^4 - 2x^3 - 5x^2 + 4x - 1=0} \\ \text{Real solutions}: \\ x=-1.89614823140755 \\ x=3.20188000352314 \\ \text{Complex solutions}: \\ x=0.347134113942206 - 0.210259195466214 i \\ x=0.347134113942206 + 0.210259195466214 i\)

\(\mathbf{x^4 - 4x^3 + 5x^2 + 2x - 1 = 0} \\ \text{Real solutions}: \\ x=-0.527384928792028 \\ x=0.312316513704344 \\ \text{Complex solutions}: \\ x=2.10753420754384 + 1.27653384988106 i \\ x=2.10753420754384 - 1.27653384988106 i\)

Help Please! Find the residue of \(182\cdot 12 - 15\cdot 7 + 3\pmod{14}\).

\(\begin{array}{|rcll|} \hline && \mathbf{182\cdot 12 - 15\cdot 7 + 3\pmod{14}} \\ &=& 2082 \pmod{14} \\ &=& 148*14 + 10 \pmod{14} \\ &=& 0 + 10 \pmod{14} \\ &=& \mathbf{ 10 \pmod{14} } \\ \hline \end{array}\)

Question

\(\begin{array}{|rcll|} \hline \mathbf{f(n)} &=& \mathbf{\log_{10}(2^n)} \\ \hline \\ && \mathbf{\dfrac{f(n)}{\log_{10}(2)}} \\\\ &=& \dfrac{\log_{10}(2^n)}{\log_{10}(2)} \\\\ &=&n \dfrac{\log_{10}(2)}{\log_{10}(2)} \\\\ &=& \mathbf{n} \\ \hline \end{array} \)

Let u, v, and w be vectors satisfying \(\mathbf{u}\bullet \mathbf{v} = 3,\ \mathbf{u} \bullet \mathbf{w} = 4,\ \mathbf{v} \bullet \mathbf{w} = 5\).

Then what are \((\mathbf{u} + 2 \mathbf{v})\bullet \mathbf{w},\ (\mathbf{w} - \mathbf{u})\bullet \mathbf{v},\ (3\mathbf{v} - 2 \mathbf{w})\bullet \mathbf{u}\) equal to?

\(\begin{array}{|rcll|} \hline \mathbf{u}\bullet \mathbf{v} = \mathbf{v}\bullet \mathbf{u} &=& 3 \\ \mathbf{u} \bullet \mathbf{w}=\mathbf{w} \bullet \mathbf{u} &=& 4 \\ \mathbf{v} \bullet \mathbf{w}=\mathbf{w} \bullet \mathbf{v} &=& 5 \\ \hline \end{array}\\ \begin{array}{|rcll|} \hline && (\mathbf{u} + 2 \mathbf{v})\bullet \mathbf{w} \\ &=& \mathbf{u} \bullet \mathbf{w}+2\mathbf{v} \bullet \mathbf{w} \\ &=& 4+2\cdot 5 \\ &=&\mathbf{ 14 } \\ \hline \end{array} \begin{array}{|rcll|} \hline && (\mathbf{w} - \mathbf{u})\bullet \mathbf{v} \\ &=& \mathbf{w} \bullet \mathbf{v} - \mathbf{u}\bullet \mathbf{v} \\ &=& 5-3 \\ &=&\mathbf{ 2 } \\ \hline \end{array} \begin{array}{|rcll|} \hline && (3\mathbf{v} - 2 \mathbf{w})\bullet \mathbf{u} \\ &=& 3\mathbf{v}\bullet \mathbf{u} - 2\mathbf{w} \bullet \mathbf{u} \\ &=& 3 \cdot 3 -2\cdot 4 \\ &=& 9-8 \\ &=&\mathbf{ 1 } \\ \hline \end{array} \)

Find the distance between the x-intercept and the y-intercept of the graph of the equation \(2x-5y=10\).

\(\begin{array}{|rcll|} \hline 2x-5y &=& 10 \quad & | \quad : 10 \\\\ \dfrac{2x}{10}-\dfrac{5y}{10} &=& 1 \\\\ \dfrac{ x}{5}-\dfrac{ y}{2} &=& 1 \\\\ \mathbf{\dfrac{ x}{5}+\dfrac{ y}{-2}} &=& \mathbf{1} \\ \hline \end{array} \)

x-intercept \(= 5\)

y-intercept \(= -2\)

The distance:

\(\begin{array}{|rcll|} \hline && \sqrt{5^2+(-2)^2} \\ &=& \sqrt{25+4} \\ &=& \mathbf{\sqrt{29}} \\ \hline \end{array}\)

Find constants A and B such that

\(\dfrac{x + 7}{x^2 - x - 2} = \dfrac{A}{x - 2} + \dfrac{B}{x + 1}\)

Please help!

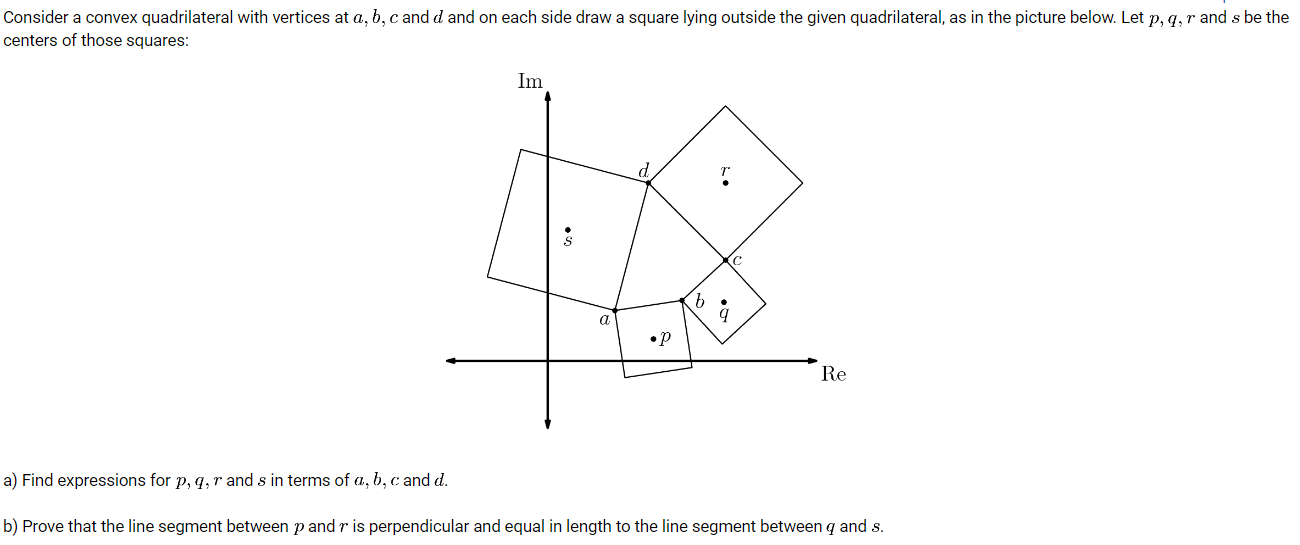
a)

Find expressions for p,q,r and s in terms of a,b,c and d

\(\begin{array}{|rcll|} \hline p &=& \dfrac{a+b}{2} + \left(\dfrac{b-a}{2}\right)_\perp \\ 2p &=& (a+b) + (b-a)_\perp \qquad \text{rotate clockwise $\times (-i)$ }\\ 2p &=& (a+b) + (b-a)\times (-i) \\ \mathbf{2p} &=& \mathbf{(a+b) + (a-b)i}\\ \text{similarly} \quad \\ \mathbf{2q} &=& \mathbf{(b+c) + (b-c)i}\\ \mathbf{2r} &=& \mathbf{(c+d) + (c-d)i}\\ \mathbf{2s} &=& \mathbf{(d+a) + (d-a)i}\\ \hline \end{array} \)

b)
Prove that the line segment between p and r
is perpendicular  to the line segment between q and s

\(\begin{array}{|rcll|} \hline 2rp &=& 2(r-p) \\ &=& 2r-2p \\ &=& (c+d)+(c-d)i-(a+b)-(a-b)i \\ &=& (c+d)-(a+b)+(c-d)i-(a-b)i \qquad (1) \\\\ 2sq &=& 2(s-q) \\ &=& 2s-2q \\ &=& (d+a)+(d-a)i-(b+c)-(b-c)i \\ &=& (d+a)-(b+c)+(d-a)i-(b-c)i \qquad (2) \\\\ \hline \mathbf{2rp_\perp} &=& \mathbf{2sq\ ?} \\ 2rp &=& (c+d)-(a+b)+(c-d)i-(a-b)i \qquad \text{rotate counter clockwise $\times i$ } \\ 2rp_\perp &=& \Big((c+d)-(a+b)+(c-d)i-(a-b)i\Big) \times i \\ 2rp_\perp &=& (c+d)i-(a+b)i+(c-d)i^2-(a-b)i^2\qquad i^2=-1 \\ 2rp_\perp &=& (c+d)i-(a+b)i-(c-d)+(a-b) \\ 2rp_\perp &=& (d+a)-(b+c)+(d-a)i-(b-c)i \\ 2rp_\perp &=& 2sq \checkmark \\ \hline \end{array} \)

Prove that the line segment between p and r
equal in length to the line segment between q and s

\(\small{ \begin{array}{|rcll|} \hline && \Big[(c+d)-(a+b)\Big]^2 +\Big[(c-d)-(a-b)\Big]^2 \\ &=&\Big[(d+a)-(b+c)\Big]^2 +\Big[(d-a)-(b-c)\Big]^2 \\\\ && (c+d)^2+(a+b)^2-2(c+d)(a+b) \\ && +(c-d)^2-(a-b)^2-2(c-d)(a-b) \\ &=& (d+a)^2+(b+c)^2-2(d+a)(b+c) \\ && +(d-a)^2+(b-c)^2-2(d-a)(b-c) \\\\ &&c^2+d^2+2cd+a^2+b^2+2ab \\ && -2ac-2bc-2da-2bd \\ && +c^2+d^2-2cd+a^2+b^2 \\ && -2ab-2ac+2bc+2da-2db \\ &=& d^2+a^2+2da+b^2+c^2+2bc \\ && -2db-2dc-2ab-2ac \\ && +d^2+a^2-2da + b^2+c^2-2bc \\ && -2db+2dc+2ab-2ac \\\\ &&c^2+d^2+a^2+b^2-2ac-2db \\ && +c^2+d^2+a^2+b^2-2ac-2db \\ &=& d^2+a^2+b^2+c^2 -2db-2ac \\ && +d^2+a^2+ b^2+c^2-2db-2ac \\\\ && 2c^2+2d^2+2a^2+2b^2-4ac-4db \\ &=& 2c^2+2d^2+2a^2+2b^2-4ac-4db\ \checkmark \\ \hline \end{array} }\)