heureka

Let \(\mathbf{u}\) and \(\mathbf{v}\) be vectors such that \(\|\mathbf{u}\| = 3\) and \(\|\mathbf{v}\| = 2\),
such that the angle between \(\mathbf{u}\) and \(\mathbf{v}\) when placed tail to tail is 60 degrees.
Let \(\mathbf{A}\) be a matrix such that \(\mathbf{row}_1(\mathbf{A}) = \mathbf{u},\ \mathbf{row}_2(\mathbf{A}) = \mathbf{v}\).
Then what are \(\mathbf{A} \mathbf{u},\ \mathbf{A} \mathbf{v}\)?

My attempt:

\(\begin{array}{|rcll|} \hline \mathbf{uv} &=& \|\mathbf{u}\|\|\mathbf{v}\|\cos{60^\circ} \\ \mathbf{uv} &=& 3*2*\dfrac12 \\ \mathbf{uv} &=& \mathbf{3} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \text{Let } \mathbf{u}&=&\dbinom{u_x}{u_y} \\ \text{Let }\mathbf{v}&=&\dbinom{v_x}{v_y} \\ \hline \mathbf{A} &=& \begin{pmatrix} u_x & u_y \\ v_x & v_y \end{pmatrix} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline \mathbf{Au} &=& \begin{pmatrix} u_x & u_y \\ v_x & v_y \end{pmatrix}\dbinom{u_x}{u_y} \\\\ \mathbf{Au} &=& \dbinom{u_x^2+u_y^2}{u_xv_x+u_yv_y} \\\\ \mathbf{Au} &=& \dbinom{\|\mathbf{u}\|^2}{\mathbf{uv}} \\\\ \mathbf{Au} &=& \dbinom{3^2}{3} \\\\ \mathbf{Au} &=& \mathbf{\dbinom{9}{3}} \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{Av} &=& \begin{pmatrix} u_x & u_y \\ v_x & v_y \end{pmatrix}\dbinom{v_x}{v_y} \\\\ \mathbf{Av} &=& \dbinom{u_xv_x+u_yv_y}{v_x^2+v_y^2} \\\\ \mathbf{Av} &=& \dbinom{\mathbf{uv}}{\|\mathbf{v}\|^2} \\\\ \mathbf{Av} &=& \dbinom{3}{2^2} \\\\ \mathbf{Av} &=& \mathbf{\dbinom{3}{4}} \\ \hline \end{array}\)

two parallel chords in a circle have lengths 10 and 14, and the distance between them is 6.

The chord parallel to these chords and midway between them is of

length \(\sqrt{a}\). Find the value of a.

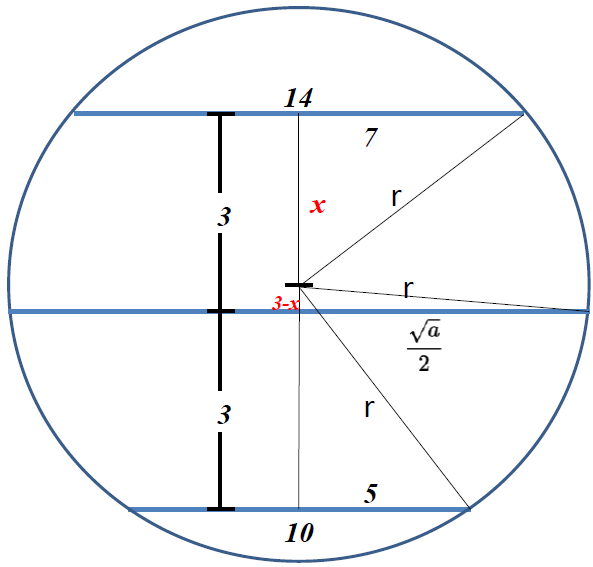
Phythagora's

\(\begin{array}{|lrcll|} \hline (1) & x^2+7^2 &=& r^2 \\ (2) & (3-x)^2 + \left(\dfrac{\sqrt{a}}{2}\right)^2 &=& r^2 \\ (3) & 5^2 + \Big(3+(3-x)\Big)^2 &=& r^2 \\ \hline \end{array} \)

\(\begin{array}{|lrcll|} \hline \mathbf{x=\ ?} \\ \hline (1)=(3): & r^2 = x^2+7^2 &=& 5^2 + \Big(3+(3-x)\Big)^2 \\ & x^2+7^2 &=& 5^2 + \Big(3+(3-x)\Big)^2 \\ & x^2+7^2 &=& 5^2 + (6-x)^2 \\ & x^2+7^2 &=& 5^2 + 6^2-12x+x^2 \\ & 7^2 &=& 5^2 + 6^2-12x \\ & 12x &=& 5^2 + 6^2 - 7^2 \\ & 12x &=& 12 \quad | \quad : 12 \\ & \mathbf{x}&=& \mathbf{1} \\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline \mathbf{r^2=\ ?} \\ \hline (1): & r^2 &=& x^2+7^2 \quad | \quad \mathbf{x=1} \\ & r^2 &=& 1^2+7^2 \\ & \mathbf{r^2}&=& \mathbf{50} \\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline \mathbf{a=\ ?} \\ \hline (2): & (3-x)^2 + \left(\dfrac{\sqrt{a}}{2}\right)^2 &=& r^2 \\ & (3-x)^2 + \dfrac{a}{4} &=& r^2 \quad | \quad \mathbf{x=1},\ \mathbf{r^2=50} \\ & (3-1)^2 + \dfrac{a}{4} &=& 50 \\ & 2^2 + \dfrac{a}{4} &=& 50 \\ & 4 + \dfrac{a}{4} &=& 50 \quad | \quad -4 \\ & \dfrac{a}{4} &=& 46 \quad | \quad * 4 \\ & \mathbf{a}&=& \mathbf{184} \\ \hline \end{array}\)

If you roll two fair six-sided dice, what is the probability that a least one dice shows a 3?

\(\begin{array}{|r|r|r|r|r|r|r|r|} \hline & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 1 & & & \color{red}\text{x} \\ 2 & & & \color{red}\text{x} \\ 3 & \color{red}\text{x} & \color{red}\text{x} & \color{red}\text{x} & \color{red}\text{x} & \color{red}\text{x} & \color{red}\text{x} \\ 4 & & & \color{red}\text{x} \\ 5 & & & \color{red}\text{x} \\ 6 & & & \color{red}\text{x} \\ \hline \end{array} \)

The probability that a least one dice shows a 3 is  \(\mathbf{\dfrac{11}{36}}\quad (30.\overline{5}\ \%)\)

In what quadrant does the terminal ray of the angle lie?

Select Quadrant I , Quadrant II , Quadrant ​ III ​, or Quadrant IV

−21π/8 

−5π/9

5π/6

35π/4

\(\begin{array}{|r|cll|} \hline \text{Quadrant} \\ \hline I. & 0^\circ \cdots 90^\circ \\ II. & 90^\circ \cdots 180^\circ \\ III.& 180^\circ \cdots 270^\circ \\ IV. & 270^\circ \cdots 360^\circ \\ \hline \end{array} \)

\(\begin{array}{|c|c|c|r|} \hline & \text{degrees} & & \text{Quadrant} \\ \hline -\dfrac{21\pi}{8} & -\dfrac{21}{8}*180^\circ=-472.5^\circ & -472.5^\circ+2*360^\circ = \mathbf{247.5^\circ} & III \\ \hline -\dfrac{5\pi}{9} & -\dfrac{5}{9}*180^\circ=-100^\circ & -100^\circ+360^\circ = \mathbf{260^\circ} & III \\ \hline \dfrac{5\pi }{6} & \dfrac{5}{6}*180^\circ=\mathbf{150^\circ} & & II \\ \hline \dfrac{35\pi }{4} & \dfrac{35}{4}*180^\circ=\mathbf{135^\circ} & & II \\ \hline \end{array}\)

Let the matrix \(\mathbf{A} = \begin{pmatrix} 1 & 2 \\ 0 & 1 \end{pmatrix}\).
Calculate \(\mathbf{A}^{10} \begin{pmatrix}1 \\ 0 \end{pmatrix},\ \mathbf{A}^{10} \begin{pmatrix}0 \\ 1 \end{pmatrix}\).

\(\begin{array}{|lrcll|} \hline \mathbf{A}^{\color{red}1} & &=& \begin{pmatrix} 1 & 2\cdot \color{red}1 \\ 0 & 1 \end{pmatrix} \\\\ \mathbf{A}^{\color{red}2} & = \begin{pmatrix} 1 & 2 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 2 \\ 0 & 1 \end{pmatrix} &=& \begin{pmatrix} 1 & 2\cdot \color{red}2 \\ 0 & 1 \end{pmatrix} \\\\ \mathbf{A}^{\color{red}3} & = \begin{pmatrix} 1 & 2 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 2\cdot 2 \\ 0 & 1 \end{pmatrix} &=& \begin{pmatrix} 1 & 2\cdot \color{red}3 \\ 0 & 1 \end{pmatrix} \\\\ \mathbf{A}^{\color{red}4} & = \begin{pmatrix} 1 & 2 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 2\cdot 3 \\ 0 & 1 \end{pmatrix} &=& \begin{pmatrix} 1 & 2\cdot \color{red}4 \\ 0 & 1 \end{pmatrix} \\\\ \cdots \\ \mathbf{A}^{\color{red}10} & &=& \begin{pmatrix} 1 & 2\cdot \color{red}10 \\ 0 & 1 \end{pmatrix} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline && \mathbf{A}^{\color{red}10}\begin{pmatrix}1 \\ 0 \end{pmatrix} \\ &=& \begin{pmatrix} 1 & 20 \\ 0 & 1 \end{pmatrix}\begin{pmatrix}1 \\ 0 \end{pmatrix} \\ &=& \begin{pmatrix}1 \\ 0 \end{pmatrix} \\ \hline \end{array} \begin{array}{|rcll|} \hline && \mathbf{A}^{\color{red}10} \begin{pmatrix}0 \\ 1 \end{pmatrix} \\ &=& \begin{pmatrix} 1 & 20 \\ 0 & 1 \end{pmatrix}\begin{pmatrix}0 \\ 1 \end{pmatrix} \\ &=& \begin{pmatrix}20 \\ 1 \end{pmatrix} \\ \hline \end{array}\)

Consider the matrices \(\begin{align*} \mathbf{A} &= \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}, \\ \mathbf{B} &= \begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix}, \\ \mathbf{C} &= \begin{pmatrix} 1 & 2 \\ 2 & -1 \end{pmatrix}. \end{align*}\)
Let \(v\) be a unit vector.
Find the magnitudes \(\|\mathbf{A}\mathbf{v}\|,\ \|\mathbf{B}\mathbf{v}\|,\ \|\mathbf{C}\mathbf{v}\|\),

or state if any of these cannot be uniquely determined from the information given.

\(\text{Let unit vector $v =\dbinom10$ }\)

\(\begin{array}{|rcll|} \hline \mathbf{A}\mathbf{v} &=& \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}\cdot\dbinom10 \\ \mathbf{A}\mathbf{v} &=& \dbinom11 \\ \|\mathbf{A}\mathbf{v}\| &=& \sqrt{1^2+1^2} \\ \mathbf{\|\mathbf{A}\mathbf{v}\|} &=& \mathbf{\sqrt{2}} \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{B}\mathbf{v} &=& \begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix}\cdot\dbinom10 \\ \mathbf{B}\mathbf{v} &=& \dbinom11 \\ \|\mathbf{B}\mathbf{v}\| &=& \sqrt{1^2+1^2} \\ \mathbf{\|\mathbf{B}\mathbf{v}\|} &=& \mathbf{\sqrt{2}} \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{C}\mathbf{v} &=& \begin{pmatrix} 1 & 2 \\ 2 & -1 \end{pmatrix}\cdot\dbinom10 \\ \mathbf{C}\mathbf{v} &=& \dbinom12 \\ \|\mathbf{C}\mathbf{v}\| &=& \sqrt{1^2+2^2} \\ \mathbf{\|\mathbf{C}\mathbf{v}\|} &=& \mathbf{\sqrt{5}} \\ \hline \end{array}\)

Let \(A\) be a matrix, and let \(x\) and \(y\) be vectors such that neither is a scalar multiple of the other and such that
\(\mathbf{A} \mathbf{x} = \mathbf{y},\ \mathbf{A} \mathbf{y} = \mathbf{x} + 2\mathbf{y}\).
Then we have that \(\mathbf{A}^{-1} \mathbf{x} = a \mathbf{x} + b\mathbf{y}\) for some scalars \(a\) and \(b\).
Find \(a\) and \(b\).

\(\begin{array}{|rcll|} \hline \mathbf{A} \mathbf{x} &=& \mathbf{y} \quad &| \quad \times \mathbf{A}^{-1} \\ \mathbf{A}^{-1}\mathbf{A}\mathbf{x} &=& \mathbf{A}^{-1} \mathbf{y} \quad &| \quad \mathbf{A}^{-1}\mathbf{A} = \text{Identity matrix} \\ \mathbf{x} &=& \mathbf{A}^{-1}\mathbf{y} \\\\ \hline \mathbf{A} \mathbf{y} &=& \mathbf{x} + 2\mathbf{y} \quad &| \quad \times \mathbf{A}^{-1} \\ \mathbf{A}^{-1}\mathbf{A}\mathbf{y} &=& \mathbf{A}^{-1}\mathbf{x} + 2\mathbf{A}^{-1} \mathbf{y} \quad &| \quad \mathbf{A}^{-1}\mathbf{A} = \text{Identity matrix} \\ \mathbf{y} &=& \mathbf{A}^{-1}\mathbf{x} + 2\mathbf{A}^{-1} \mathbf{y} \quad &| \quad \mathbf{A}^{-1}\mathbf{y} = \mathbf{x} \\ \mathbf{y} &=& \mathbf{A}^{-1}\mathbf{x} + 2\mathbf{x} \\ \mathbf{A}^{-1}\mathbf{x} &=& -2\mathbf{x}+\mathbf{y} \\ \hline \end{array}\)

\(\mathbf{a=-2,\ b=1} \)

If \(n\) is a positive integer and \((x+1)^n\) is expanded in decreasing powers of \(x\),
three consecutive numerical coefficients are in the ratio \(2:15:70\). Compute \(n\).

\(\begin{array}{|rcll|} \hline \mathbf{\dbinom{n}{k + 1}} &=& \dfrac{n!}{(k+1)!(n-k-1)!} \quad &| \quad k!(k+1)=(k+1)! \\\\ &=& \dfrac{1}{k+1} *\dfrac{n!}{k!(n-k-1)!} \quad &| \quad (n-k-1)!(n-k)=(n-k)! \\\\ &=& \dfrac{n-k}{k+1} * \dfrac{n!}{k!(n-k)!} \quad &| \quad \dfrac{n!}{k!(n-k)!} = \dbinom{n}{k} \\\\ &=& \mathbf{ \dfrac{n-k}{k+1} \dbinom{n}{k} } \\ \hline \end{array} \)

similarly \( \mathbf{\dbinom{n}{k - 1} = \dfrac{k}{n-k+1} \dbinom{n}{k} }\)

\(\begin{array}{|rcll|} \hline \dbinom{n}{k - 1} : \dbinom{n}{k} : \dbinom{n}{k + 1} &=& 2:15:70 \\\\ &&\boxed{ \mathbf{\dbinom{n}{k - 1} = \dfrac{k}{n-k+1} \dbinom{n}{k} }\\ ~\\ \mathbf{\dbinom{n}{k + 1} = \dfrac{n-k}{k+1} \dbinom{n}{k} } } \\\\ \dfrac{k}{n-k+1} \dbinom{n}{k} : \dbinom{n}{k} : \dfrac{n-k}{k+1} \dbinom{n}{k} &=& 2:15:70 \\ \hline \dfrac{\dbinom{n}{k}}{\dfrac{k}{n-k+1} \dbinom{n}{k}} &=& \dfrac{15}{2} \\\\ \dfrac{n-k+1}{k} &=& \dfrac{15}{2} \\\\ n-k+1 &=& \dfrac{15}{2}k \\ n &=& \dfrac{15}{2}k +k-1\\ \mathbf{n} &=& \mathbf{\dfrac{17}{2}k -1} \qquad (1) \\ \hline \dfrac{\dfrac{n-k}{k+1} \dbinom{n}{k} } {\dbinom{n}{k}} &=& \dfrac{70}{15} \\\\ \dfrac{n-k}{k+1} &=& \dfrac{70}{15} \\\\ 70(k+1) &=& 15(n-k) \\ 70k+70 &=& 15n-15k \\ 85k &=& 15n-70 \\ \mathbf{k} &=& \mathbf{ \dfrac{15n-70}{85} } \qquad (2) \\ \hline n &=& \dfrac{17}{2}k -1 \quad | \quad k=\dfrac{15n-70}{85} \\\\ n &=& \dfrac{17(15n-70)}{2*85}-1 \\\\ n &=& \dfrac{17(15n-70)}{170}-1 \\\\ n &=& \dfrac{ 15n-70 }{10}-1 \quad | \quad *10 \\\\ 10n &=& 15n-70-10 \\ 10n &=& 15n-80 \\ 5n &=& 80 \\ n &=& \dfrac{80}{5}\\ \mathbf{n} &=& \mathbf{16} \\\\ k &=& \dfrac{15n-70}{85} \quad | \quad n=16 \\\\ k &=& \dfrac{15*16-70}{85} \\ k &=& \dfrac{170}{85} \\ \mathbf{k} &=& \mathbf{2} \\ \hline \dbinom{n}{k - 1} : \dbinom{n}{k} : \dbinom{n}{k + 1} &=& 2:15:70 \\\\ \dbinom{16}{1} : \dbinom{16}{2} : \dbinom{16}{3} &=& 2:15:70 \\\\ 16 : 120 : 560 &=& 2:15:70 \\ \hline \end{array}\)

Let \(A\) be a matrix, and let \(x\) and \(y\) be vectors such that neither is a scalar multiple of the other and such that

\(\mathbf{A} \mathbf{x} = \mathbf{y},\ \mathbf{A} \mathbf{y} = \mathbf{x} + 2\mathbf{y}\).
Then we have that \(\mathbf{A}^5 \mathbf{x} = a \mathbf{x} + b\mathbf{y}\) for some scalars \(a\) and \(b\).
Find \(a\) and \(b\).

\(\begin{array}{|rcll|} \hline \mathbf{A} \mathbf{x} &=& \mathbf{y} \quad &| \quad \times \mathbf{A} \\ \mathbf{A}^2\mathbf{x} &=& \mathbf{A} \mathbf{y} \quad &| \quad \mathbf{A} \mathbf{y} = \mathbf{x} + 2\mathbf{y} \\ \mathbf{A}^2\mathbf{x} &=& \mathbf{x} + 2\mathbf{y} \\\\ \hline \mathbf{A}^2\mathbf{x} &=& \mathbf{x} + 2\mathbf{y} \quad &| \quad \times \mathbf{A} \\ \mathbf{A}^3\mathbf{x} &=& \mathbf{A}\mathbf{x} + 2\mathbf{A} \mathbf{y} \quad &| \quad \mathbf{A} \mathbf{x}=\mathbf{y},\ \mathbf{A} \mathbf{y} = \mathbf{x} + 2\mathbf{y} \\ \mathbf{A}^3\mathbf{x} &=& \mathbf{y} + 2( \mathbf{x} + 2\mathbf{y} ) \\ \mathbf{A}^3\mathbf{x} &=& \mathbf{y} + 2\mathbf{x} + 4\mathbf{y} \\ \mathbf{A}^3\mathbf{x} &=& 2\mathbf{x} + 5\mathbf{y} \\\\ \hline \mathbf{A}^3\mathbf{x} &=& 2\mathbf{x} + 5\mathbf{y} \quad &| \quad \times \mathbf{A} \\ \mathbf{A}^4\mathbf{x} &=& 2\mathbf{A}\mathbf{x} + 5\mathbf{A}\mathbf{y} \quad &| \quad \mathbf{A} \mathbf{x}=\mathbf{y},\ \mathbf{A} \mathbf{y} = \mathbf{x} + 2\mathbf{y} \\ \mathbf{A}^4\mathbf{x} &=& 2\mathbf{y} + 5( \mathbf{x} + 2\mathbf{y} ) \\ \mathbf{A}^4\mathbf{x} &=& 2\mathbf{y} + 5\mathbf{x} + 10\mathbf{y} \\ \mathbf{A}^4\mathbf{x} &=& 5\mathbf{x} + 12\mathbf{y} \\\\ \hline \mathbf{A}^4\mathbf{x} &=& 5\mathbf{x} + 12\mathbf{y} \quad &| \quad \times \mathbf{A} \\ \mathbf{A}^5\mathbf{x} &=& 5\mathbf{A}\mathbf{x} + 12\mathbf{A}\mathbf{y} \quad &| \quad \mathbf{A} \mathbf{x}=\mathbf{y},\ \mathbf{A} \mathbf{y} = \mathbf{x} + 2\mathbf{y} \\ \mathbf{A}^5\mathbf{x} &=& 5\mathbf{y} + 12( \mathbf{x} + 2\mathbf{y} ) \\ \mathbf{A}^5\mathbf{x} &=& 5\mathbf{y} + 12\mathbf{x} + 24\mathbf{y} \\ \mathbf{A}^5\mathbf{x} &=& 12\mathbf{x} + 29\mathbf{y} \\ \hline \end{array} \)

\(\mathbf{a=12,\ b=29}\)

Find the sum of the infinite series

\(1+2\left(\dfrac{1}{1998}\right)+3\left(\dfrac{1}{1998}\right)^2+4\left(\dfrac{1}{1998}\right)^3+\cdots\)

\(\small{ \begin{array}{rclllllllllc} & & \mathbf{1}&\mathbf{+} & \mathbf{2\left(\dfrac{1}{1998}\right)} &\mathbf{+} & \mathbf{3\left(\dfrac{1}{1998}\right)^2} &\mathbf{+} &\mathbf{ 4\left(\dfrac{1}{1998}\right)^3} & \mathbf{+}&\mathbf{\cdots} \\\\ & & & & & & & & & & &\mathbf{\text{sum }=\dfrac{a}{1-r}} \\ &=& 1&+ & 1\left(\dfrac{1}{1998}\right)^1 &+ & 1\left(\dfrac{1}{1998}\right)^2 &+ & 1\left(\dfrac{1}{1998}\right)^3 &+&\cdots & \dfrac{1}{1-\dfrac{1}{1998}} \\\\ & & &+ & 1\left(\dfrac{1}{1998}\right)^1 &+ & 1\left(\dfrac{1}{1998}\right)^2 &+ & 1\left(\dfrac{1}{1998}\right)^3 &+&\cdots & \dfrac{\left(\dfrac{1}{1998}\right)^1}{1-\dfrac{1}{1998}} \\\\ & & & & &+ & 1\left(\dfrac{1}{1998}\right)^2 &+ & 1\left(\dfrac{1}{1998}\right)^3 &+&\cdots & \dfrac{\left(\dfrac{1}{1998}\right)^2}{1-\dfrac{1}{1998}} \\\\ & & & & & & & + & 1\left(\dfrac{1}{1998}\right)^3 &+&\cdots & \dfrac{\left(\dfrac{1}{1998}\right)^3}{1-\dfrac{1}{1998}} \\\\ & & & & & & & & & +&\ldots \\ \end{array} }\)

\(\begin{array}{|rcll|} \hline &&\mathbf{ 1+2\left(\dfrac{1}{1998}\right)+3\left(\dfrac{1}{1998}\right)^2+4\left(\dfrac{1}{1998}\right)^3+\cdots } \\\\ &=& \dfrac{1}{1-\dfrac{1}{1998}} + \dfrac{\left(\dfrac{1}{1998}\right)^1}{1-\dfrac{1}{1998}} + \dfrac{\left(\dfrac{1}{1998}\right)^2}{1-\dfrac{1}{1998}} + \dfrac{\left(\dfrac{1}{1998}\right)^3}{1-\dfrac{1}{1998}} +\cdots \\\\ &=& \dfrac{1}{1-\dfrac{1}{1998}} \left( 1+ \left(\dfrac{1}{1998}\right)^1+\left(\dfrac{1}{1998}\right)^2+\left(\dfrac{1}{1998}\right)^3 +\cdots \right) \\\\ &=& \dfrac{1}{\dfrac{1998-1}{1998}} \left( 1+ \left(\dfrac{1}{1998}\right)^1+\left(\dfrac{1}{1998}\right)^2+\left(\dfrac{1}{1998}\right)^3 +\cdots \right) \\\\ &=& \dfrac{1998}{1997} \left( 1+ \left(\dfrac{1}{1998}\right)^1+\left(\dfrac{1}{1998}\right)^2+\left(\dfrac{1}{1998}\right)^3 +\cdots \right) \\\\ &=& \dfrac{1998}{1997} \left( \dfrac{1}{1-\dfrac{1}{1998}} \right) \\\\ &=& \dfrac{1998}{1997} \left( \dfrac{1}{\dfrac{1998-1}{1998}} \right) \\\\ &=& \dfrac{1998}{1997}\times \dfrac{1998}{1997} \\\\ &=& \dfrac{1998^2}{1997^2} \\\\ &=&\mathbf{ \dfrac{3992004}{3988009}} \\ \hline \end{array}\)