heureka

Let \(\mathbf{a}\), \(\mathbf{b}\), \(\mathbf{c} \) be vectors such that \(\mathbf{a} \times \mathbf{b} + \mathbf{b} \times \mathbf{c} + \mathbf{c} \times \mathbf{a} = \begin{pmatrix} -3 \\ -12 \\ 4 \end{pmatrix} \).
Find the area of the triangle whose vertices are \(\mathbf{a}\), \(\mathbf{b}\) and \(\mathbf{c} \).

\(\text{Let the area of the triangle $=A$ }\)

\(\begin{array}{|rcll|} \hline 2A &=& |~ (\mathbf{a}-\mathbf{b})\times (\mathbf{a}-\mathbf{c}) ~| \\ 2A &=& |~ \mathbf{a}\times\mathbf{a}+\mathbf{a}\times(\mathbf{-c})+(\mathbf{-b})\times\mathbf{a}+(\mathbf{-b})\times(\mathbf{-c}) ~| \\ && \boxed{ \mathbf{a}\times\mathbf{a} = 0 \\ \mathbf{a}\times(\mathbf{-c}) = \mathbf{c}\times\mathbf{a} \\ (\mathbf{-b})\times\mathbf{a} = \mathbf{a}\times\mathbf{b} \\ (\mathbf{-b})\times(\mathbf{-c}) = \mathbf{b}\times\mathbf{c} } \\ 2A &=& |~ 0+\mathbf{c}\times\mathbf{a}+\mathbf{a}\times\mathbf{b} +\mathbf{b}\times\mathbf{c} ~| \\ 2A &=& |~ \mathbf{a} \times \mathbf{b} + \mathbf{b} \times \mathbf{c} + \mathbf{c} \times \mathbf{a} ~| \\ 2A &=& |~ \begin{pmatrix} -3 \\ -12 \\ 4 \end{pmatrix} ~| \\ 2A &=& \sqrt{(-3)^2+(-12)^2+(4)^2} \\ 2A &=& \sqrt{9+144+16} \\ 2A &=& \sqrt{169} \\ 2A &=& 13 \\ A &=& \dfrac{13}{2} \\ \mathbf{A} &=& \mathbf{6.5} \\ \hline \end{array}\)

Thank you very much, Melody !

Let k be a positive real number.
The square with vertices \((k, 0)\), \((0,k)\), \((-k,0)\), and \((0,-k)\) is plotted in the coordinate plane.

Find conditions on \(a > 0\) and \(b > 0\) such that the ellipse
\(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\)
is contained inside the square (and tangent to all its sides).

\(\text{Let $x_t,y_t$ are points on the tangent line $\mathbf{y = x+k}$ from $(-k,0)$ to $(0,k)$, so $ \mathbf{y_t = x_t + k}$}\)

\(\begin{array}{|lrcll|} \hline \text{ellipse} : & \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} &=& 1 \\ \hline \text{tangent of the ellipse} : & \dfrac{x_tx}{a^2} + \dfrac{y_ty}{b^2} &=& 1 \\ & \dfrac{y_ty}{b^2} &=& 1-\dfrac{x_tx}{a^2} \\ & \ldots \\ & \mathbf{y} &=& \mathbf{\dfrac{b^2}{y_t}-\dfrac{b^2}{a^2}\dfrac{x_t}{y_t}x}\\ &&& \boxed{\text{compare with tangent line }\\ y=k+x} \\ 1. & k &=& \dfrac{b^2}{y_t} \ \text{or}\ \mathbf{b^2} = \mathbf{ky_t} \\\\ 2. & 1 &=& -\dfrac{b^2}{a^2}\dfrac{x_t}{y_t} \quad | \quad \mathbf{b^2} = \mathbf{ky_t} \\\\ & 1 &=& -\dfrac{ky_t}{a^2}\dfrac{x_t}{y_t} \\\\ & 1 &=& -\dfrac{kx_t}{a^2} \\\\ & a^2 &=& -kx_t \quad | \quad x_t = y_t -k \\ & a^2 &=& -k(y_t -k) \\ & a^2 &=& -ky_t +k^2 \\ & \mathbf{a^2} &=& \mathbf{k^2-ky_t} \\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline (1): & \mathbf{b^2} &=& \mathbf{ky_t} \\\\ (2): & \mathbf{a^2} &=& \mathbf{k^2-ky_t} \quad | \quad \mathbf{b^2=ky_t} \\ & a^2 &=& k^2-b^2 \\ & \mathbf{a^2+b^2} &=& \mathbf{k^2} \\ & \mathbf{\sqrt{a^2+b^2}} &=& \mathbf{k} \\ \hline \end{array} \)

Integration

Suppose that \(f'(x) = \dfrac{4}{\sqrt{1-x^2}}\) and that \(f(0) = 2\).
Find \(f\left(\dfrac{\sqrt{3}}{2}\right)\).

\(\begin{array}{|rcll|} \hline && \mathbf{\large{ \int } \dfrac{4}{\sqrt{1-x^2}} \ dx} \\\\ &=& 4\mathbf{\large{ \int } \dfrac{1}{\sqrt{1-x^2}} \ dx} \qquad \boxed{ \text{substitute: } \\ x = \sin(\theta),\ dx=\cos(\theta)d\theta } \\\\ &=& 4 \large{ \int } \dfrac{\cos(\theta)}{ \sqrt{1-\Big(\sin(\theta)\Big)^2} }\ d\theta \\\\ &=& 4 \displaystyle \int \dfrac{\cos(\theta)}{ \cos(\theta) }\ d\theta \\\\ &=& 4 \displaystyle \int d\theta \\ &=& 4 \theta + c \quad | \quad \theta = \arcsin(x) \\ &=& 4 \Big(\arcsin(x)\Big) + c \\ \hline f(x) &=& 4 \Big(\arcsin(x)\Big) + c \quad | \quad x=0 \\ f(0) &=& 4 \Big(\arcsin(0)\Big) + c \quad | \quad f(0) = 2 \\ 2 &=& 4 \Big(\arcsin(0)\Big) + c \\ 2 &=& 4 \cdot 0 + c \\ 2 &=& 0 + c \\ \mathbf{c} &=& \mathbf{2} \\ \hline \mathbf{f(x)} &=& \mathbf{4 \Big(\arcsin(x)\Big) + 2} \\\\ f\left(\dfrac{\sqrt{3}}{2}\right) &=& 4 \Big(\arcsin\left(\dfrac{\sqrt{3}}{2}\right)\Big) + 2 \\\\ f\left(\dfrac{\sqrt{3}}{2}\right) &=& 4\cdot \Big(\dfrac{\pi}{3}\Big) + 2 \\\\ f\left(\dfrac{\sqrt{3}}{2}\right) &=& \dfrac{4\pi}{3} + 2 \\\\ \mathbf{f\left(\dfrac{\sqrt{3}}{2}\right)} &=& \mathbf{6.18879020479} \\ \hline \end{array}\)

In trapezoid ABCD, \(\overline{AB}\parallel \overline{CD}\), and \(AB < CD\).
The base \(\overline{CD}\) has a length of \(8\).
The legs \(\overline{AD}\) and \(\overline{BC}\) have lengths of \(7\), and the diagonal \overline{BD} has a length of \(9\).
Find the area of the trapezoid.

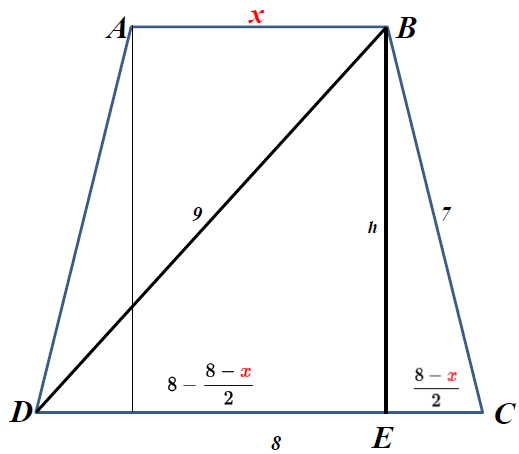
\(\text{Let $\overline{CE}=\dfrac{8-\color{red}x}{2}$} \\ \text{Let $\overline{DE}=8-\dfrac{8-\color{red}x}{2}$} \\ \text{Let $\overline{BE}=h$} \\ \text{Let $\overline{AB}=\color{red}x$} \\ \text{Let area of the trapezoid $=A $ } \)

Pythagorean Theorem:

\(\begin{array}{|rcll|} \hline \mathbf{\left(\dfrac{8-x}{2}\right)^2 + h^2} &=& \mathbf{7^2} \\\\ h^2 &=& 7^2 - \left(\dfrac{8-x}{2}\right)^2 \\\\ \mathbf{h^2} &=& \mathbf{7^2 - \dfrac{\Big(8-x\Big)^2}{4}} \qquad (1) \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\Big(8-\left(\dfrac{8-x}{2}\right)\Big)^2 + h^2} &=& \mathbf{9^2} \\\\ \left(\dfrac{16-(8-x)}{2}\right)^2 + h^2 &=& 9^2 \\\\ \left(\dfrac{8+x}{2}\right)^2 + h^2 &=& 9^2 \\\\ \dfrac{\Big(8+x\Big)^2}{4} + h^2 &=& 9^2 \\\\ \mathbf{h^2} &=& \mathbf{9^2 - \dfrac{\Big(8+x\Big)^2}{4}} \qquad (2) \\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline (1)=(2): & h^2 = 7^2 - \dfrac{\Big(8-x\Big)^2}{4} &=& 9^2 - \dfrac{\Big(8+x\Big)^2}{4} \\\\ & 7^2 - \dfrac{\Big(8-x\Big)^2}{4} &=& 9^2 - \dfrac{\Big(8+x\Big)^2}{4} \\\\ & \dfrac{\Big(8+x\Big)^2}{4} - \dfrac{\Big(8-x\Big)^2}{4} &=& 9^2-7^2 \\\\ & \dfrac{\Big(8+x\Big)^2-\Big(8-x\Big)^2}{4} &=& 32 \quad | \quad \cdot 4 \\\\ & \Big(8+x\Big)^2-\Big(8-x\Big)^2 &=& 32\cdot 4 \\\\ & 64+16x+x^2-(64-16x+x^2) &=& 32\cdot 4 \\ & 64+16x+x^2-64+16x-x^2 &=& 32\cdot 4 \\ & 16x +16x &=& 32\cdot 4 \\ & 32x &=& 32\cdot 4 \quad | \quad :32 \\ & \mathbf{ x } &=& \mathbf{4} \\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline (1): & \mathbf{h^2} &=& \mathbf{7^2 - \dfrac{\Big(8-x\Big)^2}{4}} \quad | \quad \mathbf{x=4} \\\\ & h^2 &=& 7^2 - \dfrac{\Big(8-4\Big)^2}{4} \\\\ & h^2 &=& 7^2 - \dfrac{4^2}{4} \\\\ & h^2 &=& 7^2 - 4 \\ & h^2 &=& 45 \\ & h &=& \sqrt{45} \\ & \mathbf{h} &=& \mathbf{3\sqrt{5}} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{A} &=& \mathbf{\left(\dfrac{8+x}{2}\right)\cdot h} \quad | \quad \mathbf{x=4},\ \mathbf{h=3\sqrt{5}} \\\\ A &=& \left(\dfrac{8+4}{2}\right)\cdot 3\sqrt{5} \\\\ A &=& \left(\dfrac{12}{2}\right)\cdot 3\sqrt{5} \\\\ A &=& 6\cdot 3\sqrt{5} \\\\ \mathbf{A} &=& \mathbf{18\sqrt{5}} \\\\ \mathbf{A} &=& \mathbf{40.2492235950} \\ \hline \end{array} \)

In trapezoid \(PQRS\), \(\overline{PQ} \parallel \overline{RS}\).
Let \(X\) be the intersection of diagonals \(\overline{PR}\) and \(\overline{QS}\).
The area of triangle \(PQX\) is \(20\), and the area of triangle \(RSX\) is \(45\).
Find the area of trapezoid \(PQRS\).

\(\begin{array}{|rcll|} \hline \text{Let Area }A_1 &=& [PQX] \\ A_1 &=& 20 \\\\ \text{Let Area }A_2 &=& [RSX] \\ A_2 &=& 45 \\\\ \text{Let Area }A_3 &=& [PXS] \\\\ \text{Let Area }A_4 &=& [QXR] \\\\ \text{Let Area }A_5 &=& [PSR] \\ &=& A_2+A_3 \\\\ \text{Let Area }A_6 &=& [QSR] \\ A_6 &=& A_2 +A_4 \\ \hline \mathbf{A_5} &=& \mathbf{A_6} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{A_5} &=& \mathbf{A_6} \\ A_2+A_3 &=& A_2 +A_4 \\ \mathbf{A_3 }&=& \mathbf{A_4} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline A_3 = \dfrac{SX*h_1}{2} && A_1 = \dfrac{QX*h_1}{2} \\ \mathbf{\dfrac{A_3}{A_1} }&=& \mathbf{\dfrac{SX}{QX}} \\\\ A_2 = \dfrac{SX*h_2}{2} && A_4 = \dfrac{QX*h_2}{2} \\ \mathbf{\dfrac{A_2}{A_4} }&=& \mathbf{\dfrac{SX}{QX}} \\\\ \dfrac{SX}{QX}=\mathbf{\dfrac{A_3}{A_1} }&=&\mathbf{\dfrac{A_2}{A_4} } \quad | \quad A_4 = A_3 \\\\ \dfrac{A_3}{A_1} &=& \dfrac{A_2}{A_3} \\\\ A_3^2 &=& A_1A_2 \\ A_3^2 &=& 20*45 \\ A_3^2 &=& 900 \\ \mathbf{A_3} &=& \mathbf{30} \\\\ A_4 &=& A_3 \\ \mathbf{A_4} &=& \mathbf{30} \\ \hline \end{array}\)

\(\text{The area of trapezoid $PQRS = A_1+A_2+A_3+A_4 = 20+45+30+30=\mathbf{125}$ }\)

Simplify C(n,k)/C(n,k-1)

\(\begin{array}{|rcll|} \hline \dfrac{C(n,k)} {C(n,k-1)} &=& \dfrac{ \dbinom{n}{k} }{ \dbinom{n}{k - 1} } \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\dbinom{n}{k - 1}} &=& \dfrac{n!}{(k-1)!(n-k+1)!} \quad &| \quad (k-1)!k=k!~ \text{or}~(k-1)!= \dfrac{k!}{k} \\\\ &=& k *\dfrac{n!}{k!(n-k+1)!} \quad &| \quad (n-k)!(n-k+1)=(n-k+1)! \\\\ &=& \dfrac{k}{n-k+1} * \dfrac{n!}{k!(n-k)!} \quad &| \quad \dfrac{n!}{k!(n-k)!} = \dbinom{n}{k} \\\\ &=& \mathbf{ \dfrac{k}{n-k+1} \dbinom{n}{k} } \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \dfrac{ \dbinom{n}{k} }{ \dbinom{n}{k - 1} } &=& \dfrac{ \dbinom{n}{k} }{ \dfrac{k}{n-k+1} \dbinom{n}{k} } \\\\ \dfrac{ \dbinom{n}{k} }{ \dbinom{n}{k - 1} } &=& \dfrac{1}{ \dfrac{k}{n-k+1} } \\\\ \mathbf{\dfrac{ \dbinom{n}{k} }{ \dbinom{n}{k - 1} } } &=& \mathbf{\dfrac{n-k+1}{k}} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\dfrac{C(n,k)} {C(n,k-1)}} &=& \mathbf{\dfrac{n-k+1}{k}} \\ \hline \end{array}\)

There are 10 students in a class: 6 boys and 4 girls. If the teacher picks a group of 3 at random,

what is the probability that everyone in the group is a girl?

Hypergeometric distribution:
\(\text{$N$ is the number of $\mathbf{students} = 10$}, \\ \text{$b$ is the number of $\mathbf{boys} = 6$}, \\ \text{$g$ is the number of $\mathbf{girls}= 4$}, \\ \text{$k$ the teacher picks a $\mathbf{boy} = 0 $}, \\ \text{$n$ the teacher picks a $\mathbf{girl} = 3 $}.\)

\(\begin{array}{|rcll|} \hline && \mathbf{ \dfrac{ \dbinom{b}{k} \dbinom{ g }{n} }{ \dbinom{N}{n+k} }} \\\\ &=& \dfrac{ \dbinom{6}{0}_{\text{boys}} \dbinom{4}{3}_{\text{girls}} } { \dbinom{10}{3}_{\text{all}} } \\\\ && \boxed{\dbinom{6}{0} = 1,\\ \dbinom{4}{3}=\binom{4}{4-3}=\binom{4}{1}=4,\\ \dbinom{10}{3}=\dfrac{10}{3}\cdot \dfrac{9}{2}\cdot \dfrac{8}{1} = 5\cdot 3 \cdot 8 } \\\\ &=& \dfrac{ 1\cdot 4 } { 5\cdot 3 \cdot 8 } \\\\ &=& \dfrac{ 1 } { 5\cdot 3 \cdot 2 } \\\\ &=&\mathbf{ \dfrac{ 1 } { 30 }} \\\\ &=& 0.03333333333\quad (=3.3\ \%) \\ \hline \end{array}\)

Compute the sum \(\dfrac{2}{1 \cdot 2 \cdot 3} + \dfrac{2}{2 \cdot 3 \cdot 4} + \dfrac{2}{3 \cdot 4 \cdot 5} + \cdots\)

The first term of an arithmetic sequence is −27 . The common difference of the sequence is 6.

What is the sum of the first 30 terms of the sequence?

Formula: \(\begin{array}{|rcll|} \hline a_n &=& a_1 + (n-1)d \\ s_n &=& \left(\dfrac{a_1+a_n}{2} \right)\cdot n \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{a_n} &=& \mathbf{a_1 + (n-1)d} \quad | \quad a_1=-27,\ n=30,\ d=6 \\\\ a_{30} &=& -27 + (30-1)\cdot 6 \\ a_{30} &=& -27 + 29\cdot 6 \\ a_{30} &=& -27 + 174 \\ \mathbf{a_{30}} &=& \mathbf{147} \\ \hline \mathbf{s_n} &=& \mathbf{\left(\dfrac{a_1+a_n}{2} \right)\cdot n} \quad | \quad n=30 \\\\ s_{30} &=& \left(\dfrac{a_1+a_{30}}{2} \right)\cdot 30 \quad | \quad a_1=-27,\ a_{30}=147 \\ s_{30} &=& \left(\dfrac{-27+147}{2} \right)\cdot 30 \\ s_{30} &=& \left(\dfrac{120}{2} \right)\cdot 30 \\ s_{30} &=& 60\cdot 30 \\ \mathbf{s_{30}} &=& \mathbf{1800} \\ \hline \end{array} \)