heureka

Two numbers, if the first one increases by 1, and the second one decreases by 1, then their product increases by 2020.
If the first number decreases by 1, and the second one increases by 1, what value does the product decrease?

\(\text{ Let first number $=n_1$} \\ \text{ Let second number $=n_2$}\)

\(\begin{array}{|lrcll|} \hline (1) & (n_1+1)(n_2-1) &=& n_1n_2 + 2020 \\ & n_1n_2-n_1+n_2-1 &=& n_1n_2 + 2020 \\ & -n_1+n_2-1 &=& 2020 \\ & \mathbf{ -n_1+n_2 } &=& \mathbf{ 2021 } \\ \hline (2) & (n_1-1)(n_2+1) &=& n_1n_2 + x \\ & n_1n_2+n_1-n_2-1 &=& n_1n_2 + x \\ & n_1-n_2-1 &=& x \\ & \mathbf{ n_1-n_2-1 } &=& \mathbf{ x } \\ \hline (1)+(2): & -n_1+n_2 + n_1-n_2-1 &=&2021 +x \\ & -1 &=&2021 +x \\ & x &=& -2021 -1 \\ & \mathbf{x} &=& \mathbf{-2022} \\ \hline \end{array}\)

The value of the product decreases by 2022

A regular dodecahedron \(P_1 P_2 P_3 \dotsb P_{12}\) is inscribed in a circle with radius 1.
Compute  \((P_1 P_2)^2 + (P_1 P_3)^2 + \dots + (P_{11} P_{12})^2\).
(The sum includes all terms of the form \((P_i P_j)^2\), where \(1 \le i < j \le 12\).

Let \(f(x)\)  be a polynomial such that \(f(0) = 4\), \(f(1) = 5\), and \(f(2)=10\).
Find the remainder (=r) when \(f(x)\) is divided by \(x(x - 1)(x - 2)\).

Chords \(\overline{UV}\), \(\overline{WX}\), and \(\overline{YZ}\) of a circle are parallel.
The distance between chords \(\overline{UV}\) and \(\overline{WX}\) is 4,
and the distance between chords \(\overline{WX}\) and \(\overline{YZ}\) is also 4.
If \(\overline{UV}\) = 78 and \(\overline{YZ}\) = 50, then find \(\overline{WX}\).

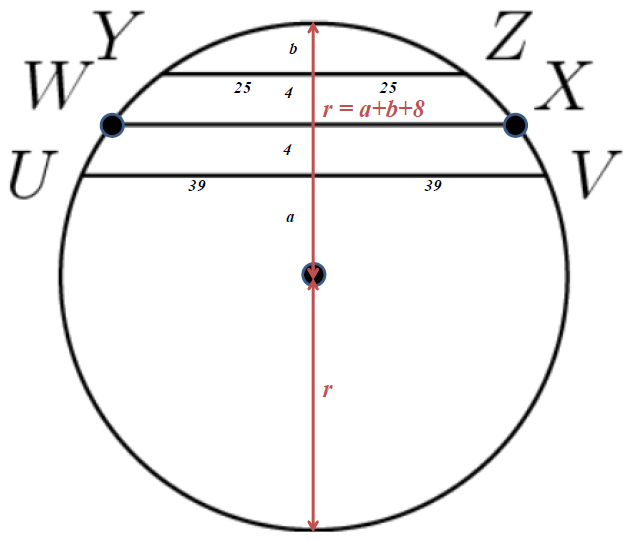
\(\begin{array}{|lrcll|} \hline (1) & \mathbf{r} &=& \mathbf{a+b+8} \\ \hline & \mathbf{39^2} &=& \mathbf{(b+8)(a+r)} \\ & 39^2 &=& (b+8)(a+a+b+8) \\ (2) & \mathbf{39^2} &=& \mathbf{(b+8)(2a+b+8)} \\ \hline & \mathbf{25^2} &=& \mathbf{b(8+a+r)} \\ & 25^2 &=& b(8+a+a+b+8) \\ (3) & \mathbf{25^2} &=& \mathbf{b(2a+b+16)} \\ \hline & \left(\dfrac{\overline{WX}}{2}\right)^2 &=& (b+4)(4+a+r) \\ & \left(\dfrac{\overline{WX}}{2}\right)^2 &=& (b+4)(4+a+a+b+8) \\ (4) & \mathbf{\left(\dfrac{\overline{WX}}{2}\right)^2} &=& \mathbf{(b+4)(2a+b+12)} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline (3): & \mathbf{25^2} &=& \mathbf{b(2a+b+16)} \\ & 625 &=& b(2a+b+16) \\ & 625 &=& 2ab+b(b+16) \\ & 2ab &=& 625- b(b+16) \\ & \mathbf{a} &=& \mathbf{\dfrac{625- b(b+16)}{2b}} \\ \hline \end{array} \)

\(\begin{array}{|lrcll|} \hline (2): & \mathbf{39^2} &=& \mathbf{(b+8)(2a+b+8)} \\ & 1521 &=& (b+8)(2a+b+8) \quad | \quad \mathbf{a=\dfrac{625- b(b+16)}{2b}} \\ & 1521 &=& (b+8)\left(2\dfrac{\Big(625- b(b+16)\Big)}{2b}+b+8 \right) \\ & 1521 &=& (b+8)\left(\dfrac{ 625- b(b+16) }{b}+b+8 \right) \\ & 1521 &=& (b+8)\left(\dfrac{625}{b}- (b+16)+b+8 \right) \\ & 1521 &=& (b+8)\left(\dfrac{625}{b}-8 \right) \\ & 1521 &=& (b+8)\dfrac{(625-8b)}{b} \\ & 1521b &=& (b+8)( 625-8b) \\ & 1521b &=& 625b-8b^2+8*625-64b \\ & 8b^2 + 960b - 5000 &=& 0 \quad | \quad : 8 \\ & \mathbf{b^2 + 120b - 625} &=& \mathbf{0} \\ \hline &b &=& \dfrac{-120\pm \sqrt{120^2-4*(-625) } }{2} \\ &b &=& \dfrac{-120\pm \sqrt{16900} }{2} \\ &b &=& \dfrac{-120\pm 130 }{2} \\\\ &\mathbf{b} &=& \mathbf{\dfrac{-120+ 130 }{2}} \\ &\mathbf{b} &=& \mathbf{5} \\\\ &\mathbf{b} &=& \mathbf{\dfrac{-120- 130 }{2}} \quad | \quad \text{no solution } b < 0!\\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline \mathbf{a} &=& \mathbf{\dfrac{625- b(b+16)}{2b}} \quad | \quad \mathbf{b=5} \\\\ a &=& \dfrac{625- 5(5+16)}{2*5} \\\\ a &=& \dfrac{625- 5*21}{10} \\\\ a &=& \dfrac{625- 105}{10} \\\\ a &=& \dfrac{520}{10} \\\\ \mathbf{a} &=& \mathbf{52} \\ \hline \end{array}\)

\(\mathbf{\overline{WX}=\ ?}\)

\(\begin{array}{|rcll|} \hline (4): & \mathbf{\left(\dfrac{\overline{WX}}{2}\right)^2} &=& \mathbf{(b+4)(2a+b+12)} \quad | \quad a=52,\ b=5 \\ & \left(\dfrac{\overline{WX}}{2}\right)^2 &=& (5+4)(2*52+5+12) \\ & \left(\dfrac{\overline{WX}}{2}\right)^2 &=& 9*121 \\ & \left(\dfrac{\overline{WX}}{2}\right)^2 &=& 1089 \\\\ & \dfrac{\overline{WX}}{2} &=& \sqrt{1089} \\\\ & \dfrac{\overline{WX}}{2} &=& 33 \\\\ &\mathbf{\overline{WX}} &=& \mathbf{66} \\ \hline \end{array}\)

In the diagram, \(\angle U = 30^\circ\), arc XY is \(170^\circ\), and arc VW is \(110^\circ\).

Find arc WY, in degrees.

\(\begin{array}{|rcll|} \hline \mathbf{\text{ In $\triangle $ UWY}} \\ \hline \mathbf{180^\circ} &=& \mathbf{U + \left(90^\circ-\dfrac{170^\circ}{2}+ 90^\circ-\dfrac{WY}{2}\right)} \\ && \quad \mathbf{ +\left(90^\circ-\dfrac{110^\circ}{2}+ 90^\circ-\dfrac{WY}{2} \right)} \\\\ 180^\circ &=& U + \left(180^\circ-85^\circ-\dfrac{WY}{2}\right) \\ && \quad + \left(180^\circ-55^\circ-\dfrac{WY}{2} \right) \\\\ 180^\circ &=& U + 95^\circ-\dfrac{WY}{2} + 125^\circ-\dfrac{WY}{2} \\\\ 180^\circ &=& U + 220^\circ - WY \quad | \quad U=30^\circ \\ 180^\circ &=& 30^\circ + 220^\circ - WY \\ 180^\circ &=& 250^\circ - WY \\ WY &=& 250^\circ - 180^\circ \\ \mathbf{WY} &=& \mathbf{70^\circ} \\ \hline \end{array}\)

Let
\(A = \dfrac{10^{1998} + 1}{10^{1999} + 1}\) and \(B=\dfrac{10^{1999} + 1}{10^{2000} + 1}\)

Which value is larger?

\(\begin{array}{|rcll|} \hline \mathbf{B} &=& \mathbf{ \dfrac{10^{1999} + 1}{10^{2000} + 1} } \\\\ B &=& \dfrac{10*10^{1998} + 1}{10*10^{1999} + 1} \\\\ B &=& \dfrac{10*\left(10^{1998} + \frac{1}{10} \right)}{10*\left(10^{1999} + \frac{1}{10}\right)} \\\\ \mathbf{B} &=& \mathbf{ \dfrac{10^{1998} + \frac{1}{10} }{10^{1999} + \frac{1}{10}} } \\ \hline \end{array}\)

\(\Rightarrow A \gt B\)

2.
Let \(f(x)\)  be a polynomial such that \(f(0) = 4\), \(f(1) = 5\), and \(f(2)=10\).
Find the remainder \((=r)\) when \(f(x)\) is divided by \(x(x - 1)(x - 2)\).

\(\begin{array}{|lrclrcl|} \hline & f(x) &=& q(x)*x(x - 1)(x - 2) + r \quad | \quad \mathbf{r=ax^2+bx+c } \\ & \mathbf{ f(x) } &=& \mathbf{ q(x)*x(x - 1)(x - 2) + ax^2+bx+c } \\ \hline x=0:& \mathbf{ f(0) } &=& \mathbf{ q(0)*0(0 - 1)(0 - 2) + a*0^2+b*0+c } \\ & f(0)&=& q(0)*0 +c \\ & f(0)&=& c \quad | \quad f(0) = 4 \\ & 4&=& c \\ & \mathbf{c} &=& \mathbf{4} \\ \hline x=1:& \mathbf{ f(1) } &=& \mathbf{ q(1)*1(1 - 1)(1 - 2) + a*1^2+b*1+c } \\ & f(1)&=& q(1)*0 a+b+4 \\ & f(1)&=& a+b+4 \quad | \quad f(1) = 5 \\ & 5&=& a+b+4 \\ & \mathbf{a+b} &=& \mathbf{1} \qquad (1) \\ \hline x=2:& \mathbf{ f(2) } &=& \mathbf{ q(2)*2(2 - 1)(2 - 2) + a*2^2+b*2+c } \\ & f(2)&=& q(2)*0 +4a+2b+4 \\ & f(2)&=& 4a+2b+4 \quad | \quad f(2) = 10 \\ & 10&=& 4a+2b+4 \quad | \quad :2 \\ & 5&=& 2a+b+2 \\ & \mathbf{2a+b} &=& \mathbf{3} \qquad (2) \\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline & \mathbf{a+b} &=& \mathbf{1} \qquad (1) \\ & \mathbf{2a+b} &=& 3 \qquad (2) \\ \hline (2)-(1): & 2a+b -(a+b) &=& 3-1 \\ & \mathbf{a} &=& \mathbf{2} \\ \hline & b &=& 1-a \\ & b &=& 1-2 \\ & \mathbf{b} &=& \mathbf{-1} \\ \hline & r &=& ax^2+bx+c \\ & \mathbf{ r } &=& \mathbf{2x^2-x+4} \\ \hline \end{array} \)

The remainder when \(f(x)\) is divided by \(x(x - 1)(x - 2)\) is  \(\mathbf{2x^2-x+4}\)

1.

\(f(x) = x^{10}+5x^9-8x^8+7x^7-x^6-12x^5+4x^4-8x^3+12x^2-5x-5\)
 

Without using long division, find the remainder \((=r)\)  when \(f(x)\)  is divided by \(x^2-1\).

Let \(x^2-1 = (x-1)(x+1)\)

\(\begin{array}{|lrclrcl|} \hline & f(x) &=& q(x)(x-1)(x+1) + r \quad | \quad \mathbf{r=ax+b} \\ & \mathbf{ f(x) } &=& \mathbf{ q(x)(x-1)(x+1) + ax+b } \\ \hline x=1:& \mathbf{ f(1) } &=& \mathbf{ q(1)(1-1)(1+1) + a*1+b } \\ & f(1)&=& q(1)*0 + a+b \\ & f(1)&=& a+b \\ &&& \small {f(1) = 1*1^{10}+5*1^9-8*1^8+7*1^7-1^6-12*1^5+4*1^4-8*1^3+12*1^2-5*1-5 }\\ &&& f(1) = 1+5-8+7-1-12+4-8+12-5-5 \\ &&& f(1) = -8+7+4-8-5 \\ &&& f(1) = 11-21 \\ &&& f(1) = -10 \\ & -10 &=& a+b \\ & \mathbf{a+b} &=& \mathbf{-10} \qquad (1) \\ \hline x=-1:& \mathbf{ f(-1) } &=& \mathbf{ q(-1)(-1-1)(-1+1) + a*(-1)+b } \\ & f(-1)&=& q(-1)*0 - a+b \\ & f(-1)&=& - a+b \\ &&& \small{f(-1) = 1*(-1)^{10}+5*(-1)^9-8*(-1)^8+7*(-1)^7-(-1)^6-12*(-1)^5+4*(-1)^4-8*(-1)^3+12*(-1)^2-5*(-1)-5} \\ &&& f(-1) = 1-5-8-7-1+12+4+8+12+5-5 \\ &&& f(-1) =12+4 \\ &&& f(-1) = 16 \\ & 16 &=& - a+b \\ & \mathbf{-a+b} &=& \mathbf{16} \qquad (2)\\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline & \mathbf{a+b} &=& \mathbf{-10} \qquad (1) \\ & \mathbf{-a+b} &=& \mathbf{16} \qquad (2)\\ \hline (1)+(2): & a+b-a+b&=&-10+16 \\ & 2b&=& 6 \\ & \mathbf{b} &=& \mathbf{3} \\ \hline (1)-(2): & a+b-(-a+b) &=& -10-16 \\ & 2a &=& -26 \\ & \mathbf{a} &=& \mathbf{-13} \\ \hline & r &=& ax+b \\ & \mathbf{ r } &=& \mathbf{-13x+3} \\ \hline \end{array}\)

The remainder when \(f(x)\) is divided by \(x^2-1\) is \(\mathbf{-13x+3}\)