heureka

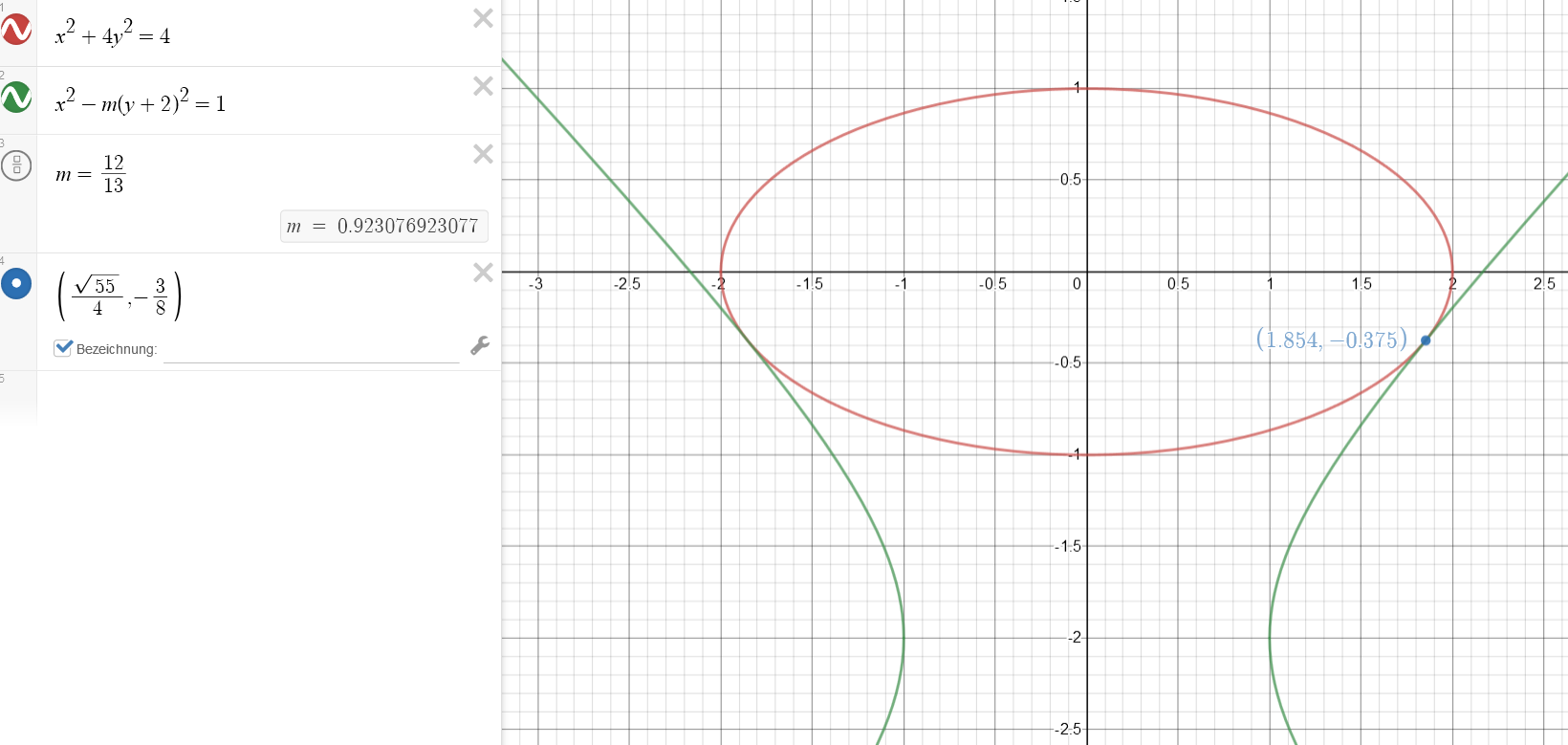
The ellipse \(x^2 +4y^2 =4\) and the hyperbola \(x^2 -m(y+2)^2 =1\) are tangent.

Compute \(m\)

My attempt

1. The coordinate of the ellipse and the hyperbola must be the same

\(\begin{array}{|rcll|} \hline \mathbf{x^2+4y^2} &=& \mathbf{4} \\ \mathbf{x^2} &=& \mathbf{4-4y^2} \\ \hline \mathbf{x^2 -m(y+2)^2} &=& \mathbf{1} \quad | \quad \mathbf{x^2=4-4y^2} \\ \mathbf{4-4y^2 -m(y+2)^2} &=& \mathbf{1} \qquad (1) \\ \hline \end{array}\)

2. The slope at the ellipse and at the hyperbola must be equal

\(\begin{array}{|rcll|} \hline \text{The slope at the ellipse} \\ \hline \dfrac{\partial f(x,y)} {\partial x} &=& 2x \\ \dfrac{\partial f(x,y)} {\partial y} &=& 8y \\ && \boxed{\text{Formula: }\\ \dfrac{dy}{dx} = -\dfrac{\dfrac{\partial f} {\partial x}} {\dfrac{\partial f} {\partial y}} } \\\\ \dfrac{dy}{dx} &=& -\dfrac{ 2x } { 8y } \\\\ \mathbf{ \dfrac{dy}{dx}} &\mathbf{=}& \mathbf{-\dfrac{ x } { 4y }} \\ \hline \end{array} \begin{array}{|rcll|} \hline \text{The slope at the hyperbola} \\ \hline \dfrac{\partial f(x,y)} {\partial x} &=& 2x \\ \dfrac{\partial f(x,y)} {\partial y} &=& -2m(y+2)*1 \\ && \boxed{\text{Formula: }\\ \dfrac{dy}{dx} = -\dfrac{\dfrac{\partial f} {\partial x}} {\dfrac{\partial f} {\partial y}} } \\\\ \dfrac{dy}{dx} &=& -\dfrac{ 2x } { -2m(y+2) } \\\\ \mathbf{ \dfrac{dy}{dx}} &\mathbf{=}& \mathbf{\dfrac{ x } {m(y+2) }} \\ \hline \end{array}\\ \begin{array}{|rcll|} \hline \mathbf{ \dfrac{dy}{dx}} = \mathbf{-\dfrac{ x } { 4y }} &\mathbf{=}& \mathbf{\dfrac{ x } {m(y+2) }}\\ -\dfrac{ x } { 4y } &=& \dfrac{ x } {m(y+2) }\\ -\dfrac{ 1 } { 4y } &=& \dfrac{ 1 } {m(y+2) }\\ m(y+2) &=& -4y \\ \mathbf{m} &=& \mathbf{-\dfrac{4y}{y+2} } \\ \hline \end{array} \)

\(\begin{array}{|lrcll|} \hline (1): & \mathbf{4-4y^2 -m(y+2)^2} &=& \mathbf{1} \quad | \quad \mathbf{m=-\dfrac{4y}{y+2} } \\ & 4-4y^2 +\dfrac{4y}{(y+2)}(y+2)^2 &=& 1 \\ & 4-4y^2 +4y(y+2) &=& 1 \\ & 4-4y^2 +4y^2+8y &=& 1 \\ & 4 +8y &=& 1 \\ & 8y &=& -3 \\ & \mathbf{y} &=&\mathbf{ -\dfrac{3}{8}} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline \mathbf{m} &=& \mathbf{-\dfrac{4y}{y+2} } \quad | \quad \mathbf{y=-\dfrac{3}{8}} \\\\ m &=& -\dfrac{4\left(-\dfrac{3}{8}\right) }{-\dfrac{3}{8}+2} \\\\ m &=& \dfrac{ \dfrac{3}{2} }{2-\dfrac{3}{8}} \\\\ m &=& \dfrac{3}{2}\above 1pt \dfrac{13}{8} \\ \\ m &=& \dfrac{3}{2} * \dfrac{8}{13} \\\\ \mathbf{m} &=& \mathbf{\dfrac{12}{13}} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{x^2} &=& \mathbf{4-4y^2} \quad | \quad \mathbf{y=-\dfrac{3}{8}} \\\\ x^2&=& 4-4\left(\dfrac{3}{8}\right)^2 \\\\ x^2&=& 4-\dfrac{4*9}{64} \\\\ x^2&=& 4-\dfrac{9}{16} \\\\ x^2&=& \dfrac{64-9}{16} \\\\ x^2&=& \dfrac{55}{16} \\\\ \mathbf{x} &=& \mathbf{ \dfrac{\sqrt{55}}{4} } \\ \hline \end{array}\)

1. Find the quotient and remainder when x^2+2 is divided by x-2.

2. Find the quotient and remainder when 9x^4+x^3-12x+21 is divided by x+4.

In how many different ways can \(\dfrac{2}{15}\) be represented as \(\dfrac1a + \dfrac1b\), if a and b are positive integers with \(a \ge b\)?

Randomly choose two numbers between 0 and 1. What is the probability that their average is no greater than 2/3?

There are three squares inside the triangle .

Find the area of the third triangle with steps , please

\(\begin{array}{|rcl|} \hline \tan(\varphi) &=& \dfrac{4}{p_1} \qquad \tan(\varphi) = \dfrac{q_1}{4} \\ \hline p_1+q_1 &=& 4\left(\dfrac{1}{\tan(\varphi)}+\tan(\varphi) \right) \\ \hline \end{array} \begin{array}{|rclcrcl|} \hline \tan(\varphi) &=& \dfrac{3}{p_2} \qquad \tan(\varphi) = \dfrac{q_2}{3} \\ \hline p_2+q_2 &=& 3\left(\dfrac{1}{\tan(\varphi)}+\tan(\varphi) \right) \\ \hline \end{array}\\ \begin{array}{|rcll|} \hline \sin(\varphi)&=& \dfrac{x}{p_1+q_1+4} \\ \sin(\varphi)&=& \dfrac{x}{4\left(\dfrac{1}{\tan(\varphi)}+\tan(\varphi) \right)+4} \\ 4\sin(\varphi)&=& \dfrac{x}{ \dfrac{1}{\tan(\varphi)}+\tan(\varphi) +1} \\ \dfrac{1}{\tan(\varphi)}+\tan(\varphi)+1 &=& \dfrac{x}{4\sin(\varphi)}\\ \hline \end{array} \begin{array}{|rcll|} \hline \cos(\varphi)&=& \dfrac{x}{p_2+q_2+3} \\ \cos(\varphi)&=& \dfrac{x}{3\left(\dfrac{1}{\tan(\varphi)}+\tan(\varphi) \right)+3} \\ 3\cos(\varphi)&=& \dfrac{x}{\dfrac{1}{\tan(\varphi)}+\tan(\varphi) +1} \\ \dfrac{1}{\tan(\varphi)}+\tan(\varphi) +1 &=& \dfrac{x}{3\cos(\varphi)}\\ \hline \end{array}\\ \begin{array}{|rcll|} \hline \dfrac{x}{4\sin(\varphi)} &=& \dfrac{x}{3\cos(\varphi)}\\ \mathbf{\tan(\varphi)} &=& \mathbf{\dfrac{3}{4}} \\ && \Rightarrow \cos(\varphi) = \dfrac{4}{\sqrt{3^2+4^2}} \\ && \Rightarrow \mathbf{\cos(\varphi) = \dfrac{4}{5} } \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline x &=& 3\cos(\varphi) \left(\dfrac{1}{\tan(\varphi)}+\tan(\varphi) +1\right) \\\\ x &=& \dfrac{3*4}{5} \left(\dfrac{1}{ \dfrac{3}{4} }+\dfrac{3}{4} +1\right) \\\\ x &=& \dfrac{3*4}{5} \left(\dfrac{4}{3}+\dfrac{3}{4} +1\right) \\\\ x &=& \dfrac{4}{5} \left(4+\dfrac{9}{4} +3\right) \\\\ x &=& \dfrac{4}{5} \left(7+\dfrac{9}{4} \right) \\\\ x &=& \dfrac{4}{5} * \dfrac{37}{4} \\\\ x &=& \dfrac{37}{5} \\\\ \mathbf{x} &=& \mathbf{7.4} \\ \mathbf{x^2} &=& \mathbf{54.76\ \text{cm}^2} \\ \hline \end{array}\)

The area of the third triangle is \(\mathbf{54.76\ \text{cm}^2}\)

Simplify 

\(0^2 \dbinom{n}{0} + 1^2 \dbinom{n}{1} + 2^2 \dbinom{n}{2} + 2^3 \dbinom{n}{2} + \dots + (n-1)^2 \dbinom{n}{n-1}+ n^2 \dbinom{n}{n}\),

where \(n \ge 2\).

\(\begin{array}{|rcll|} \hline \mathbf{S} &=& \mathbf{0^2 \dbinom{n}{0} + 1^2 \dbinom{n}{1} + 2^2 \dbinom{n}{2} + 2^3 \dbinom{n}{2} + \dots + (n-1)^2 \dbinom{n}{n-1}+ n^2 \dbinom{n}{n} } \\\\ \mathbf{S} &=& \mathbf{\sum \limits_{k=0}^{n} k^2\dbinom{n}{k} } \\\\ S &=& \sum \limits_{k=0}^{n} k*k*\dbinom{n}{k} \quad | \quad \mathbf{k = \dbinom{k}{1}} \\\\ S &=& \sum \limits_{k=0}^{n} k\dbinom{k}{1}\dbinom{n}{k} \quad | \quad \color{red}\dbinom{k}{1}\dbinom{n}{k}= \dbinom{n}{1}\dbinom{n-1}{k-1} \\\\ S &=& \sum \limits_{k=1}^{n} k\dbinom{n}{1}\dbinom{n-1}{k-1} \quad | \quad \mathbf{\dbinom{n}{1}=n } \\\\ S &=& \sum \limits_{k=1}^{n} kn\dbinom{n-1}{k-1} \\\\ \mathbf{S} &=& \mathbf{ n\sum \limits_{k=1}^{n} k\dbinom{n-1}{k-1} }\\ \hline \end{array}\)

\(\mathbf{ \sum \limits_{k=1}^{n} k\dbinom{n-1}{k-1} = \ ? }\)

\(\begin{array}{|rcll|} \hline \mathbf{\left( 1+x \right)^{n-1}} &=& \mathbf{\dbinom{n-1}{0}x^0 +\dbinom{n-1}{1}x^1 + \dbinom{n-1}{2}x^2 + \dots + \dbinom{n-1}{n-1}x^{n-1}} \quad | \quad *x \\\\ x\left( 1+x \right)^{n-1} &=& \dbinom{n-1}{0}x^1 +\dbinom{n-1}{1}x^2 + \dbinom{n-1}{2}x^3 + \dots + \dbinom{n-1}{n-1}x^{n} \\\\ x\left( 1+x \right)^{n-1} &=& \sum \limits_{k=0}^{n-1} \dbinom{n-1}{k}x^{k+1} \\\\ \dfrac{d}{dx}x\left( 1+x \right)^{n-1} &=& \sum \limits_{k=0}^{n-1} (k+1) \dbinom{n-1}{k}x^{k} \\\\ x(n-1) \left(1+x \right)^{n-2} + \left( 1+x \right)^{n-1} &=& \sum \limits_{k=0}^{n-1} (k+1) \dbinom{n-1}{k}x^{k} \quad | \quad \mathbf{x=1} \\\\ (n-1) \left(1+1 \right)^{n-2} + \left( 1+1 \right)^{n-1} &=& \sum \limits_{k=0}^{n-1} (k+1) \dbinom{n-1}{k}1^{k} \\\\ (n-1) \left(2 \right)^{n-2} + \left( 2 \right)^{n-1} &=& \sum \limits_{k=0}^{n-1} (k+1) \dbinom{n-1}{k} \\\\ (n-1) 2^{n-2} + 2^{n-1} &=& \mathbf{\sum \limits_{k=1}^{n} k \dbinom{n-1}{k-1}} \\ \hline \end{array}\)

\(\mathbf{S= \ ?} \)

\(\begin{array}{|rcll|} \hline \mathbf{S} &=& \mathbf{ n\sum \limits_{k=1}^{n} k\dbinom{n-1}{k-1} } \quad | \quad \mathbf{\sum \limits_{k=1}^{n} k \dbinom{n-1}{k-1} = (n-1) 2^{n-2} + 2^{n-1} }\\\\ S &=& n\left( (n-1) 2^{n-2} + 2^{n-1} \right) \\\\ S &=& n\left( (n-1) 2^{n-2} + 2^{n-1}*\dfrac{2}{2} \right) \\\\ S &=& n\left( (n-1) 2^{n-2} + 2^{n-2}*2 \right) \\\\ S &=& n2^{n-2}\left( n-1 + 2 \right) \\\\ S &=& n2^{n-2}\left( n+1 \right) \\\\ \mathbf{S} &=& \mathbf{n(n+1)2^{n-2}} \quad | \quad f(n)= n(n+1),\ g(n) = n-2,\ n \ge 2\\ \hline \end{array}\)

Randomly choose two numbers between 0 and 1.
What is the probability that their mean is no greater than 2/3?

\(\text{Let number one $= x$ } \\ \text{Let number two $= y$ } \\ \text{Let the mean $= \dfrac{x+y}{2}$ } \)

Their mean is no greater than \(\dfrac{2}{3}\):
\(\dfrac{x+y}{2} \le \dfrac{2}{3}\)

\(\begin{array}{|rcll|} \hline \dfrac{x+y}{2} &=& \dfrac{2}{3} \\ x+y &=& \dfrac{4}{3} \quad | \quad y=1 \\ x+1 &=& \dfrac{4}{3} \\ x &=& \dfrac{4}{3}-1 \\ \mathbf{x} &=& \mathbf{\dfrac{1}{3}} \\ \hline \end{array} \begin{array}{|rcll|} \hline \dfrac{x+y}{2} &=& \dfrac{2}{3} \\ x+y &=& \dfrac{4}{3} \quad | \quad x=1 \\ 1+y &=& \dfrac{4}{3} \\ y &=& \dfrac{4}{3}-1 \\ \mathbf{y} &=& \mathbf{\dfrac{1}{3}} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline \text{The probability} &=& \dfrac{A_{\color{red}red}}{A} \\\\ && A_{\color{red}red} = \dfrac{\left(1+\frac13\right)}{2}*\dfrac23+\dfrac13*1 \\\\ && \mathbf{A_{\color{red}red} = \dfrac{7}{9}} \\\\ && A = 1*1 \\\\ && \mathbf{A = 1} \\\\ \text{The probability} &=& \dfrac{\frac{7}{9}}{1} \\\\ \mathbf{\text{The probability}} &=& \mathbf{\dfrac{7}{9}} \\ \hline \end{array}\)

The sides of triangle XYZ are XY = XZ = 25 and YZ = 40.

A semicircle is inscribed in triangle XYZ so that its diameter lies on \(\overline{YZ}\), and is tangent to the other two sides.

Find the area of the semicircle.

Three balls are placed inside a cone such that each ball is in contact with the edge of the cone and the next ball.

If the radii of the balls are 20 cm, 12 cm, and r cm from top to bottom, what is the value of r?

\(\begin{array}{|llllll|} \hline &\mathbf{ \dfrac{x+r}{r} } &=& \mathbf{ \dfrac{x+2r+12}{12} } &=& \mathbf{ \dfrac{x+2r+2*12+20}{20} } \\\\ &\dfrac{x+r}{r} &=& \dfrac{x+2r+12}{12} &=& \dfrac{x+2r+44}{20} \\ \hline \end{array}\\ \begin{array}{|lrcl|} \hline 1. & \mathbf{ \dfrac{x+r}{r}} &=& \mathbf{ \dfrac{x+2r+12}{12} } \\\\ & 12(x+r) &=& r(x+2r+12) \\ & 12x+12r &=& rx+2r^2+12r \\ & 12x &=& rx+2r^2 \\ & 12x-rx &=& 2r^2 \\ & x(12-r) &=& 2r^2 \\ & \mathbf{ x } &=& \mathbf{ \dfrac{2r^2} {12-r} } \\ \hline \end{array} \begin{array}{|lrcl|} \hline 2. & \mathbf{ \dfrac{x+r}{r}} &=& \mathbf{ \dfrac{x+2r+44}{20} } \\\\ & 20(x+r) &=& r(x+2r+44) \\ & 20x+20r &=& rx+2r^2+44r \\ & 20x-rx &=& 2r^2+24r \\ & x(20-r) &=& 2r^2+24r \\ & \mathbf{ x } &=& \mathbf{ \dfrac{2r^2+24r } {20-r} } \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{ x = \dfrac{2r^2} {12-r} } &=& \mathbf{ \dfrac{2r^2+24r } {20-r} } \\\\ \dfrac{2r^2} {12-r} &=& \dfrac{2r^2+24r } {20-r} \\\\ (2r^2) (20-r) &=& (12-r) (2r^2+24r) \\\\ 40r^2-2r^3 &=& 24r^2+12*24r-2r^3-24r^2 \\ 40r^2 &=& 12*24r \quad | \quad :r \\ 40r &=& 12*24 \quad | \quad :40 \\\\ r &=& \dfrac{12*24} {40} \\\\ \mathbf{ r } &=& \mathbf{7.2\ \text{cm}} \\ \hline \end{array}\)