Melody

Yes that is really good.  I am glad my steps helped.

I assume you rearranged the circle formulas for yourself ?

Here is a pic (which you already know)

Hi OrangeJuice.

Welcome to our web2.0calc forum 

I have no idea how you got sqrt24 but this is what you need to do

1) these are both circles.  So get them into centre-radius form.  Have you done that yet?  What did you get?

2) find the distance between the central points - (you should be able to see that the circles do not overlap)

3) subrtact the 2 radii.

It fell out nicely for me, with no sqrts in the final answer.  I have not checked my answer though.

If you want more help then please interact with me.  If I am not around I am sure someone else will fill the void.

**

Please no one race in with a final answer.  Teaching answers are usually best.

Here is the question

I have looked at this question but this sentence does not make any sense.  Not to me anyway.

" Points C and D are parallel to AC meets CB extended at E "

How can points be parallel to anything ?????

I might as well put my 2 cents worth in as well  

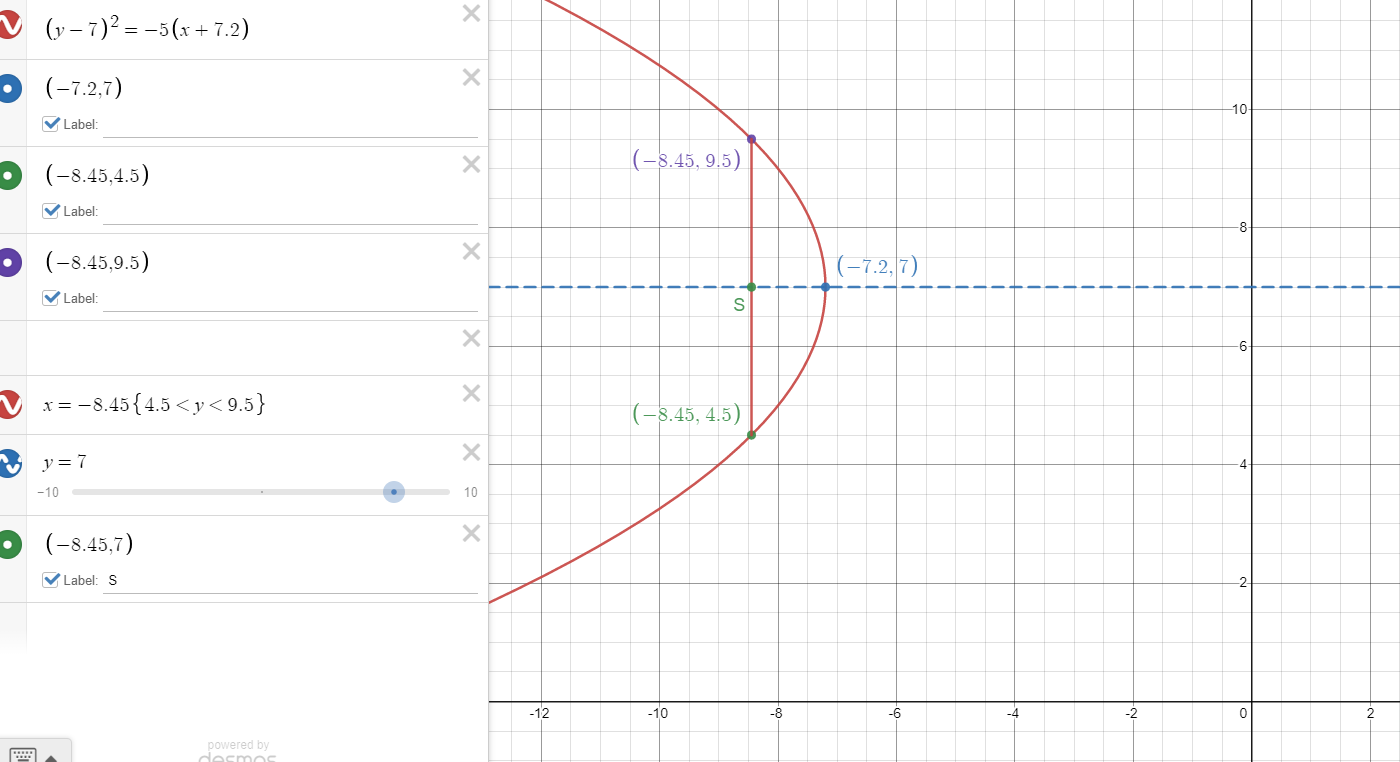
Find the vertex of the graph of the equation x - y^2 + 8y = 13 + 6x - 6y.

\(x - y^2 + 8y = 13 + 6x - 6y\\ -y^2+6y + 8y = 13 + 6x -x\\ - y^2+14y = 5x+13\\ y^2-14y = -5x-13\\ y^2-14y+49 = -5x-13+49\\ (y-7)^2 = -5x+36\\ (y-7)^2 = -5(x+7.2)\\ (y-7)^2 = -4*\frac{5}{4}(x+7.2)\\ \)

This is a sideways parabola opening in the negative x direction.

It has a vertex of (-7.2,7)

It has a focal length of  5/4

So the focal point is  

The length of the latus r****m is 5

LaTex

x - y^2 + 8y = 13 + 6x - 6y\\
 -y^2+6y + 8y = 13 + 6x -x\\
- y^2+14y = 5x+13\\
 y^2-14y = -5x-13\\
 y^2-14y+49 = -5x-13+49\\
(y-7)^2 = -5x+36\\
(y-7)^2 = -5(x+7.2)\\
(y-7)^2 = -4*\frac{5}{4}(x+7.2)\\

It is just Pythagoras's theorem.

the x value is the horizontal distance from (0,0)

the y value is the vertical distance from (0,0)

these are at right angles to each other.

If you add the squares of these you get the square of the hypotenuse.   

If the hypotenuse is 1 (that is what unit circle means)  you get

x^2+y^2 = 1  

Maybe you can use better words  

Hi Dudeman,

I can see why but not without a fair amount of effort.

Do you have a short cut method?

Good logic guest but you need to be very careful to read the question properly and answer what is asked.

Hi Orange Juice,

"For starters, only numbers that divide over 2 or 5 are terminating decimals."

What about 4 or 8 or any power of 2 or any power of 5 or any power of 10 ..................   

Ohhh ....  do  you mean the denominator must be a power of 2 or a power of 5 or a power of 10 .........

Mmmm not sure what you mean ..............

4T + 3C = 21

3T + 4C = 16

Multiply the fist one by 3 and the second one by 4

12T+9C=63

12T+16C=64

Subtract the first one FROM the second one

7C = 1

C = 1/7

2C=2/7

check

4T+3/7 = 21

4T = 20 +4/7

T= 5 and 1/7

Put into the second equation

3*(5+1/7)+ 4(1/7)

=15+3/7 + 4/7

=16

Works perfectly.

Your question is not complete