CPhill

Absolute  Minimum  =  (-3, -18)

Local Max  =   (-1,2)

So ......  increasing from  (-3, -1)

Local Min  =  (1, - 2)

So......decreasing from  ( -1, 1)

Local Max   = (3,18)

So.....increasing from ( 1, 3)  

You are correct, Juloius.....!!!

-4, 1 and 2 are the x intercepts of the graph

So.....  "D"  is the correct graph

Log N  = 5.6

Exponential  Form:  10^5.6  = N

b = 10

x  = 5.6

n  = N 

antilog  =  398107.17   

Sorry, AC....I saw the first one yesterday....but I don't know what the "2.5" represents....maybe someone else knows....!!!!

However.....all is not lost....!!!!.....here's my answer to the second one  :

https://web2.0calc.com/questions/help-asap-plz#r2

Draw  DE  perpendicular to  AB

Then  ADE  forms a right triangle  with  AE  =  (21 -9 ) / 2   = 12/2  =  6

Now....cos angle DAE  = (6/10)  =  3/5

And angle ABC  is supplemental to this...so its cos  =  -3/5

And we can use the Law of Cosines to find AC

AC  =  sqrt  [ AD^2 + DC^2  - 2(AD * DC)cos (ABC) ]

AC  = sqrt [ 10^2  + 9^2 - 2 (10 * 9) (-3/5) ]

AC  = sqrt [ 181  + 108 ]

AC = sqrt [289 ] =    17

√12   =  √[4 * 3]  =  2√3

√25  =  5

√30     can't be simplified further

√100  = 10

√10     can't be simplified further

√14     can't be simplified further

√9  = 3

Draw  QM intersecting  RT  at M  and parallel to T

Then.....triangle RQM  is right  with  angle RQM  = 10°

Then  we have that

sin (RQM)  =  RM / QR   

sin (10°)  = RM / QR   

QR sin (10°)  =  RM

Then....the height of Q above the ground is given by :

RT  -  RM  =

RT - QRsin (10° )

Just put this into the calculator  ≈  2.7945   (rounded )

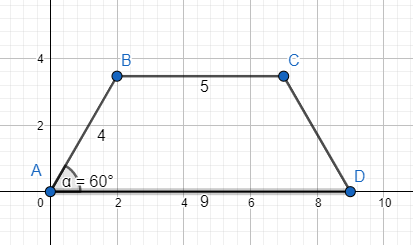
Since this is an isosceles trapezoid.....the non-parallel sides are equal

The length of one of the sides, S, is the hypotenuse of a right triangle and is given by

sin (60) = 2sqrt(3)  / S

sqrt (3) / 2  =  2sqrt (3) / S

1/2  = 2/S      rearrange  as

S  =  2 / (1/2)   = 4

Call the other leg of this triangle, L

And the length of L  can be found as follows :

tan (60) = 2sqrt (3) / L

sqrt (3)  = 2sqrt (3)  /L

1  = 2 / L

L  = 2

And due to symmetry...the length of the longer base is  5  + 2L  =  9

So.....the perimeter  is    5  + 2(4) +  9    =     22  in

Here's a pic, ACG :

Probability  of   two kings  =  C(4,2) / C(52, 2)

Probability  of at least one ace =   1  - P (no aces)  =   1 - C(48, 2)  / C(52, 2)

So......total probability  is

[ C(4,2)/C(52, 2) ]   +  [ 1  - C(48,2)   / C(52,2)]  =    2 / 13